 |
Langley Research CenterTurbulence Modeling Resource |
K-e-zeta-f Turbulence Model
This web page gives detailed information
on the equations for the three-equation (plus elliptic relaxation equation, for a total of four equations) k-e-zeta-f turbulence closure.
All forms of the model given on this page are linear eddy viscosity models.
Linear models use the Boussinesq assumption for the constitutive relation:
Unless otherwise stated, for compressible flow with heat transfer this model is implemented as described on the page
Implementing Turbulence Models into the Compressible RANS Equations, with perfect gas
assumed and Pr = 0.72, Prt = 0.90, and Sutherland's law for dynamic viscosity.
Return to: Turbulence Modeling Resource Home Page K-e-zeta-f2004 Model
(k-e-zeta-f2004)
This model's references are:
Note the latter reference has a typo in the equation for the time scale, T.
This model is based on original ideas of Durbin (see, e.g., the k-e-v2-f model as described in
AIAA Journal, Vol. 33, No. 4, 1995, pp. 659-664,
https://doi.org/10.2514/3.12628).
Note that This model (written in conservation form) is given
by the following:
Non-locality is represented by an elliptic relaxation equation for f:
Note for incompressible flows, the production term exactly becomes:
(which is often taken as a good approximation except for very high Mach numbers;
see Notes on Running the Cases with CFD, note 4).
Here, The turbulent eddy viscosity is computed from:
The time scale and length scale are computed from:
The closure coefficients are:
There are no specific farfield boundary conditions recommended for this model.
At the wall, the
boundary conditions are:
with d = distance to the wall, and numerical implementation details for the limit terms are unspecified
in the original papers.
As implied in Kalitzin (AIAA 99-3780), a typical implementation for these terms might be:
where the subscript "1" indicates the value at the first interior grid point or cell center above the wall.
Note that another common wall BC used for
where (Although not described in detail here, it is also possible to manipulate the
See Hanjalic and Launder, Modelling Turbulence in Engineering and the Environment,
Cambridge University Press, 2011, sections 6.2 and 7.4.)
Return to: Turbulence Modeling Resource Home Page
Responsible NASA Official:
Ethan Vogel
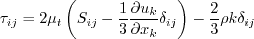
 .
The k-e-zeta-f2004 model is also described
online at:
.
The k-e-zeta-f2004 model is also described
online at:
![\frac{\partial \rho k}{\partial t} +
\frac{\partial (\rho u_j k)}{\partial x_j} = P - \rho \varepsilon +
\frac{\partial}{\partial x_j} \left[
\left( \mu + \frac{\mu_t}{\sigma_k} \right) \frac{\partial k}{\partial x_j} \right]](k-e-zeta-f_eqns/img2.png)
![\frac{\partial \rho \varepsilon}{\partial t} +
\frac{\partial (\rho u_j \varepsilon)}{\partial x_j} =
\frac{C_{\varepsilon 1} P - C_{\varepsilon 2} \rho \varepsilon}{T}
+ \frac{\partial}{\partial x_j} \left[
\left( \mu + \frac{\mu_t}{\sigma_{\varepsilon}} \right) \frac{\partial \varepsilon}{\partial x_j} \right]](k-e-zeta-f_eqns/img3.png)
![\frac{\partial \rho \zeta}{\partial t} +
\frac{\partial (\rho u_j \zeta)}{\partial x_j} = \rho f - \frac{\zeta}{k}P +
\frac{\partial}{\partial x_j} \left[
\left( \mu + \frac{\mu_t}{\sigma_{\zeta}} \right) \frac{\partial \zeta}{\partial x_j} \right]](k-e-zeta-f_eqns/img4.png)
where
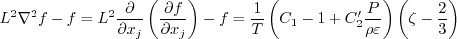
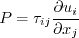
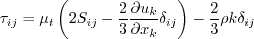
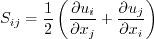
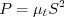
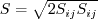 .
.
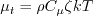
![T = {\rm max} \left[ {\rm min} \left(
\frac{k}{\varepsilon}, \frac{0.6}{\sqrt{6} C_{\mu} |S| \zeta} \right),
C_T \left( \frac{\nu}{\varepsilon} \right)^{1/2} \right]](k-e-zeta-f_eqns/img12.png)
![L = C_L {\rm max} \left[ {\rm min} \left(
\frac{k^{3/2}}{\varepsilon},
\frac{k^{1/2}}{\sqrt{6} C_{\mu} |S| \zeta} \right),
C_{\eta} \left( \frac{\nu^3}{\varepsilon} \right)^{1/4} \right]](k-e-zeta-f_eqns/img13.png)
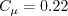
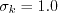
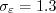
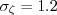
![C_{\varepsilon 1} = 1.4[1+(0.012/\zeta)]](k-e-zeta-f_eqns/img18.png)
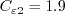
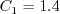
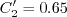


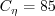
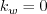
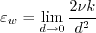

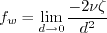
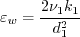
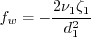
 is:
is:
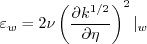
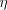 is the
direction normal to the wall (see Hanjalic and Launder, Modelling Turbulence in Engineering and the Environment,
Cambridge University Press, 2011, section 6.2).
is the
direction normal to the wall (see Hanjalic and Launder, Modelling Turbulence in Engineering and the Environment,
Cambridge University Press, 2011, section 6.2).
 and f equations so that
and f equations so that
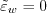 and
and
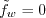 , using
, using
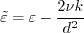
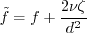
Page Curator:
Clark Pederson
Last Updated: 11/08/2021