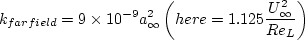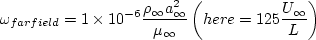Results are shown here from 2 compressible codes
so that the user may compare their own compressible code results. Multiple grids were
used so the user can see trends with grid refinement. Different codes will behave
differently with grid refinement depending on many factors (including code order of accuracy
and other numerics),
but it would be expected that as the grid is refined the results
will tend toward an "infinite grid" solution that is the same.
Be careful when comparing details: any differences in boundary conditions or flow conditions
may affect results.
Two independent compressible RANS codes,
CFL3D and FUN3D, were used to compute this
zero-pressure-gradient flat plate flow with the Menter shear stress transport model
(version SST-Vm - see full description on
Menter Shear Stress Transport page). The full series of 5 grids were used.
CFL3D is a cell-centered structured-grid code, and FUN3D
is a node-centered unstructured-grid code (FUN3D can solve on mixed element grids, so this case
was computed on the same hexahedral grid used by CFL3D). Both codes used Roe's Flux Difference
Splitting and a UMUSCL upwind approach. In CFL3D its standard UMUSCL (kappa=0.33333) scheme was
used, whereas in FUN3D the option UMUSCL 0.5 was used. Both codes were run with
full Navier-Stokes (as opposed to thin-layer, which is CFL3D's default mode of operation),
and both codes used first-order upwinding for the advective terms of the turbulence model.
Details about the codes can be found on their respective websites,
the links for which are given on this site's
home page.
The codes were not run to machine-zero iterative convergence, but an attempt was made to converge
sufficiently so that results of interest were well within normal engineering tolerance and
plotting accuracy. For example, for CFL3D the density residual was typically
driven down below 10-13. It should be kept in mind that many of the files given below
contain computed values directly from the codes,
using a precision greater than the convergence tolerance (i.e., the values
in the files are not necessarily as precise as the number of digits given).
Note that in the SST-Vm model, in the production

the second term is not included. For this particular low-speed flow, the effect of this second term
is negligible, so SST-V and SST-Vm results are essentially the same.
(Previously on this page the results were reported as SST-V solutions, but more properly they should be referred
to as SST-Vm.)
For the CFL3D and FUN3D tests reported below, the turbulent inflow boundary conditions used for SST-Vm
were the following:
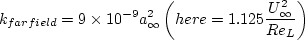
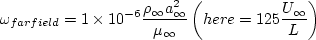
where the second equality (in parentheses) is shown solely for the purpose of relating the farfield BCs in CFL3D and
FUN3D to the nondimensionalizations used in the
original SST reference. This relation applies for the current problem only (M=0.2, Re=5 million).
This is because (for example) the k in CFL3D and FUN3D is a nondimensional
quantity (k' = k/ainf2), which is by default set to 9.e-9 in the freestream.
Furthermore, ReL, which in the context of the
original SST reference
is supposed to relate to the "approximate length of the computational
domain," is taken here as
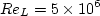 .
.
The above two equations represent the "standard" SST-Vm boundary condition
values used by both CFL3D and FUN3D, chosen to achieve
a not-too-low level of freestream
turbulent kinetic energy, a not-too-severe rate of freestream turbulence decay,
and a reasonable level of freestream turbulent eddy viscosity of
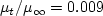 .
Although these levels are different from the range quoted in the
original SST reference,
tests were also done with the following levels that fall within the original SST author's recommended range:
.
Although these levels are different from the range quoted in the
original SST reference,
tests were also done with the following levels that fall within the original SST author's recommended range:
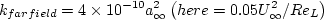 , and
, and
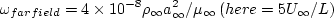 . The resulting freestream turbulent eddy viscosity ends up
about the same:
. The resulting freestream turbulent eddy viscosity ends up
about the same:
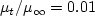 .
Computed results were almost identical (for example, both
Cf in the middle of the plate and total CD differed by well less than
one percent). See further discussion near the bottom of the page (below) on influence of freestream
turbulence levels for this case.
.
Computed results were almost identical (for example, both
Cf in the middle of the plate and total CD differed by well less than
one percent). See further discussion near the bottom of the page (below) on influence of freestream
turbulence levels for this case.
For the interested reader, typical input files for this problem are given here:
CFL3D V6.5:
FUN3D (original):
FUN3D (new - should yield nearly the same converged results as original):
All FUN3D results below are from the original run (rev 32421).
Note: prior to April 2, 2010, the drag coefficient numbers posted on this page were scaled too high by a
factor of 2, because an incorrect reference area (of 1 instead of 2) was used. This has been corrected here.
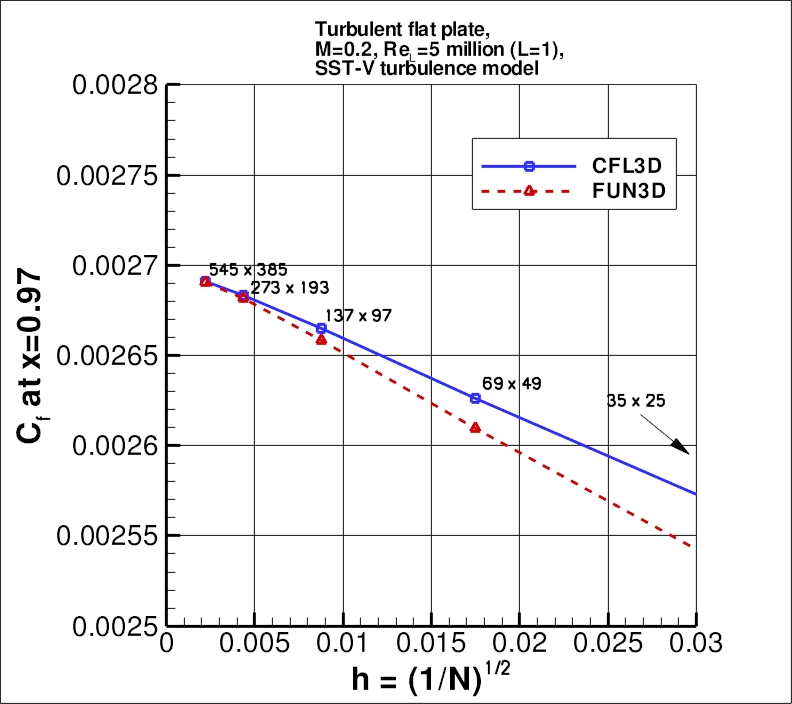
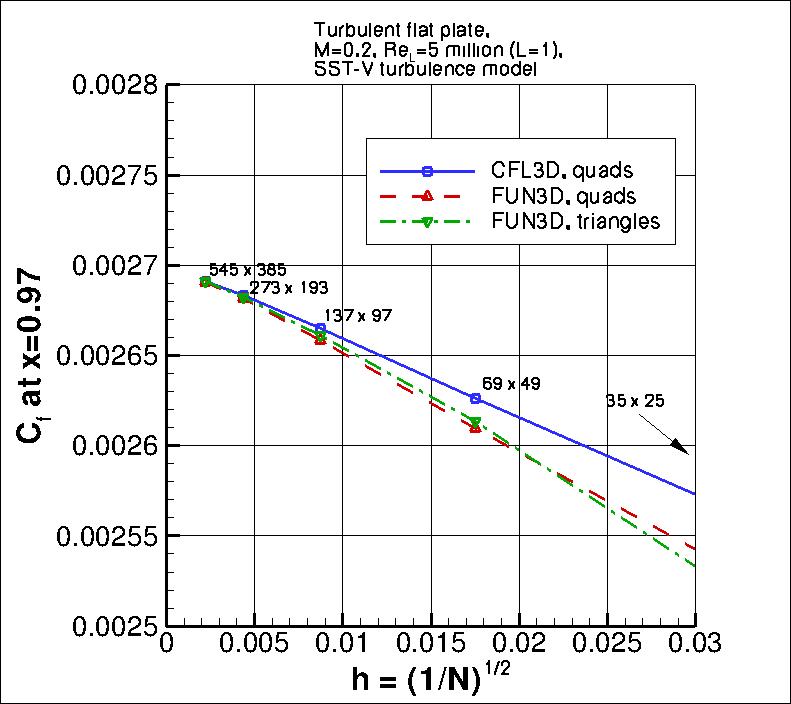
The following plot shows the convergence of the wall skin friction coefficient at x=0.97008 with
grid size for the two codes.
In the plot the x-axis is plotting 1/N1/2, which is proportional to
grid spacing (h).
At the left of the plot, h=0 represents an infinitely fine grid.
As can be seen, both codes go toward approximately the same result on an infinitely refined grid.
Using the uncertainty estimation procedure from the Fluids Engineering Division of the ASME (Celik, I. B.,
Ghia, U., Roache, P. J., Freitas, C. J., Coleman, H., Raad, P. E.,
"Procedure for Estimation and Reporting of Uncertainty Due
to Discretization in CFD Applications," Journal of Fluids Engineering, Vol. 130, July 2008, 078001, https://doi.org/10.1115/1.2960953), described in Summary of Uncertainty Procedure,
the finest 3 grids yield the following for skin friction coefficient at x=0.97:
| Code |
Computed apparent order, p |
Approx rel fine-grid error, ea21 |
Extrap rel fine-grid error, eext21 |
Fine-grid convergence index, GCIfine21 |
| CFL3D |
1.21 |
0.292% |
0.221% |
0.277% |
| FUN3D |
1.39 |
0.330% |
0.204% |
0.256% |
The data file that generated the above plot is given here:
cf_convergence_sstv.dat.
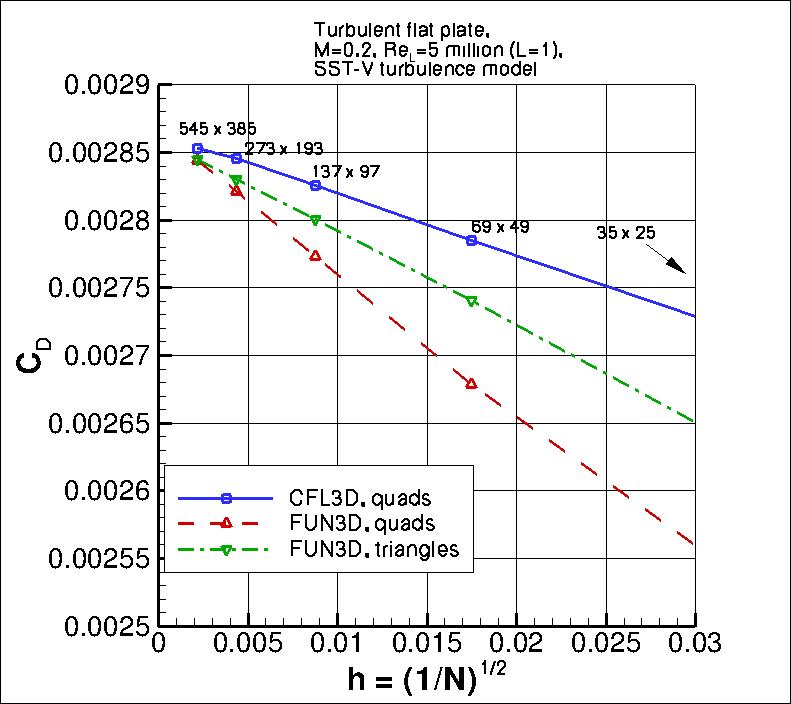
Note that in this particular flat plate case, when looking at the total integrated drag coefficient on the plate,
formal order-property convergence may not be generally achievable. This is because the skin friction
(which is the only contributor to the drag in this case)
is singular (tends toward infinity) at the leading edge. The finer the grid, the more nearly singular
the local behavior on a finite grid. FUN3D, which is a node-centered code, solves for flow variables
at the leading edge, so it may be more sensitive to the singular behavior than CFL3D, which is a
cell-centered code. There also appears to be some locally minor
anomalous behavior at the aft end of the plate, which is likely a function of
how each code handles the interaction of the solid wall boundary condition with the
outflow pressure boundary condition near the bottom right corner of the grid.
Nonetheless, both codes are tending toward a similar integrated drag coefficient value
as the grid is refined.
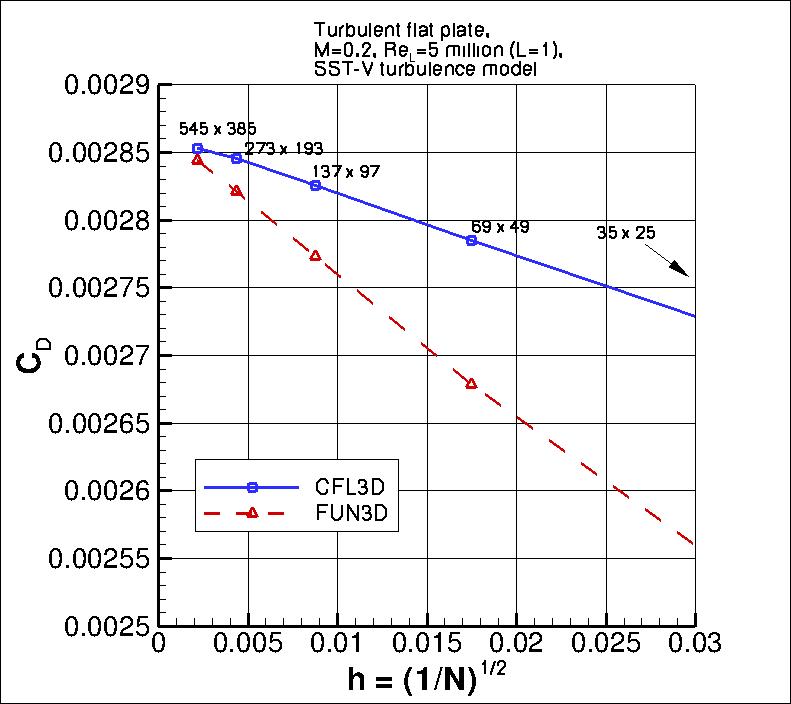
Using the uncertainty estimation procedure from the Fluids Engineering Division of the ASME (Celik, I. B.,
Ghia, U., Roache, P. J., Freitas, C. J., Coleman, H., Raad, P. E.,
"Procedure for Estimation and Reporting of Uncertainty Due
to Discretization in CFD Applications," Journal of Fluids Engineering, Vol. 130, July 2008, 078001, https://doi.org/10.1115/1.2960953), described in Summary of Uncertainty Procedure,
the finest 3 grids yield the following for drag coefficient:
| Code |
Computed apparent order, p |
Approx rel fine-grid error, ea21 |
Extrap rel fine-grid error, eext21 |
Fine-grid convergence index, GCIfine21 |
| CFL3D |
1.34 |
0.272% |
0.177% |
0.222% |
| FUN3D |
1.07 |
0.804% |
0.726% |
0.914% |
The data file that generated the above plot is given here:
drag_convergence_sstv.dat.
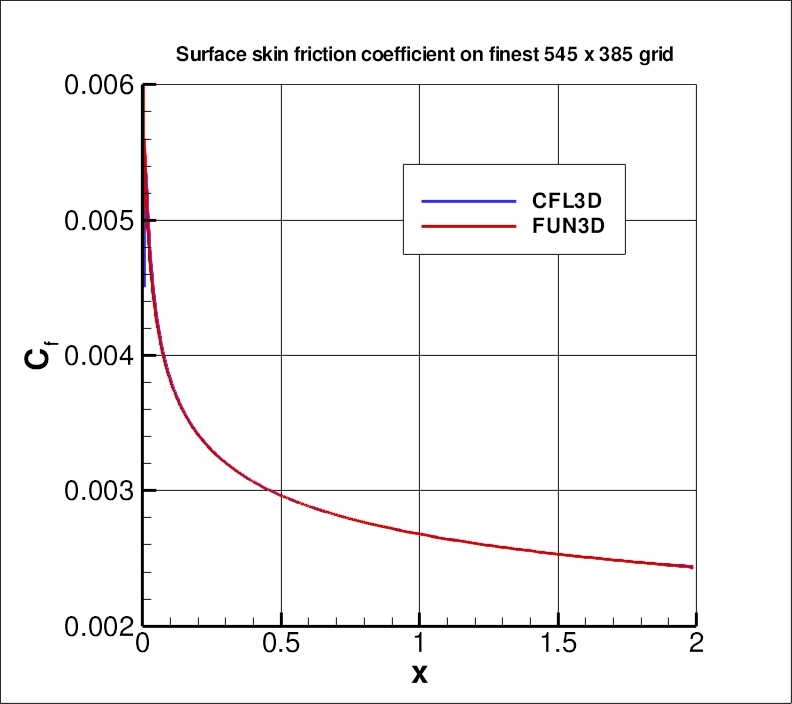
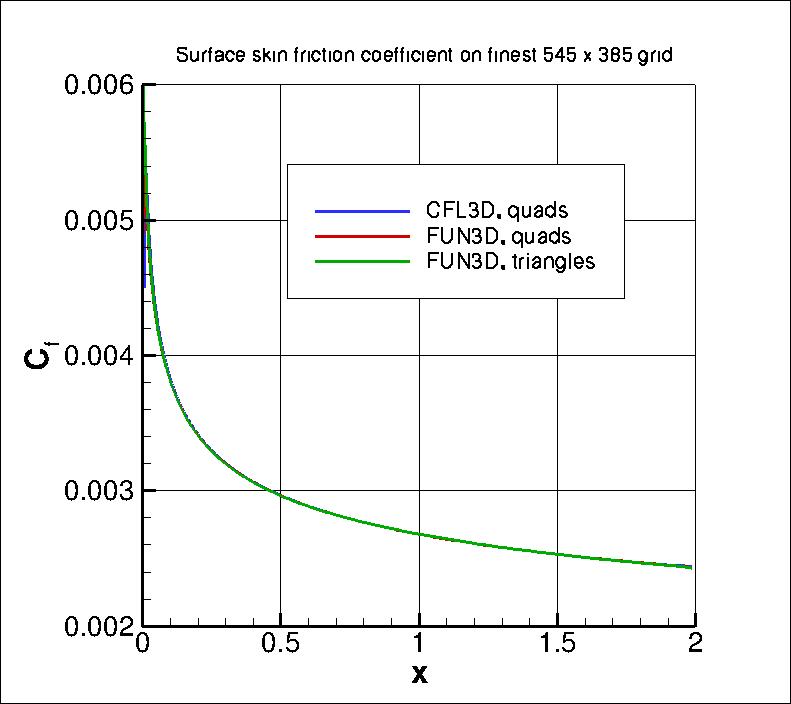
The surface skin friction coefficient from both codes on the finest 545 x 385 grid
over the entire plate is shown in the next plot. Again, local anomalous behavior exists near the leading
edge (x=0) due to singular behavior of the solution,
and near the trailing edge (x=2) most likely due to boundary condition
interaction. These behaviors differ for the two codes, and result in small local deviations that
can be seen when zoomed into the two locations. In addition, both codes indicate turbulence
"activation" at slightly different locations very near the leading edge, 0 < x < 0.01
("activation" is where the turbulence model transitions
on its own from laminar to turbulent). But both codes are seen to yield nearly identical results
over most of the plate.
The data file that generated the above plot is given here:
cf_plate_sstv.dat.
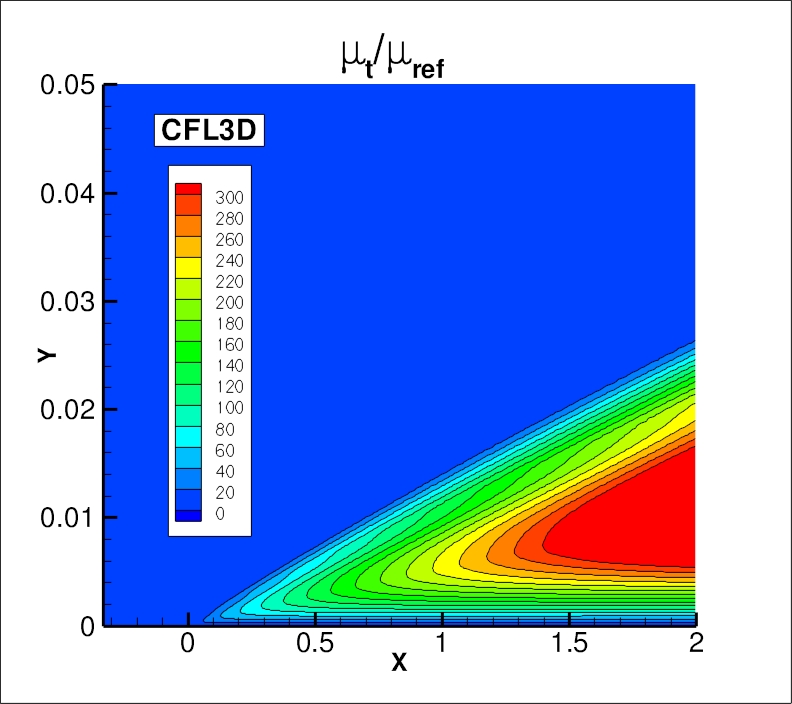
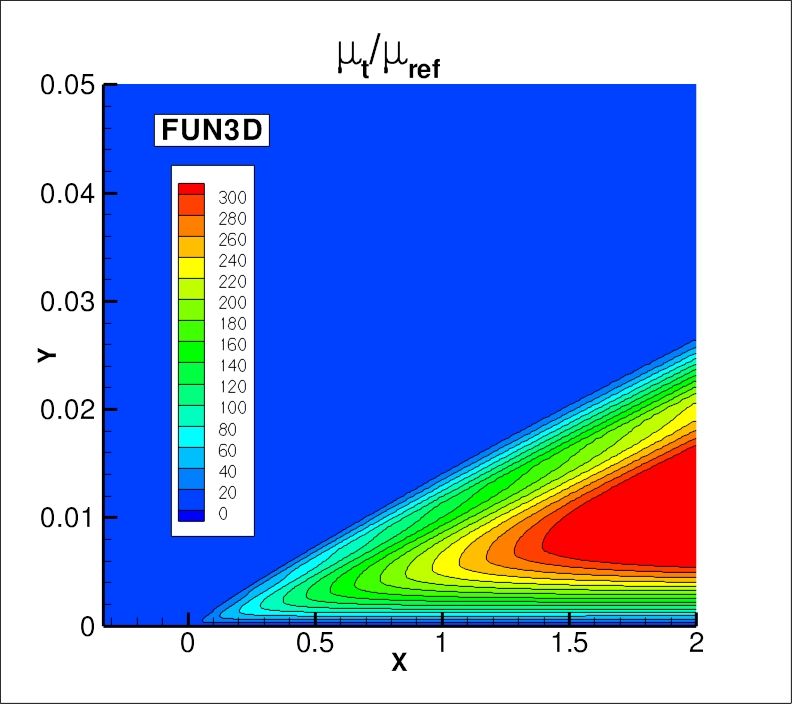
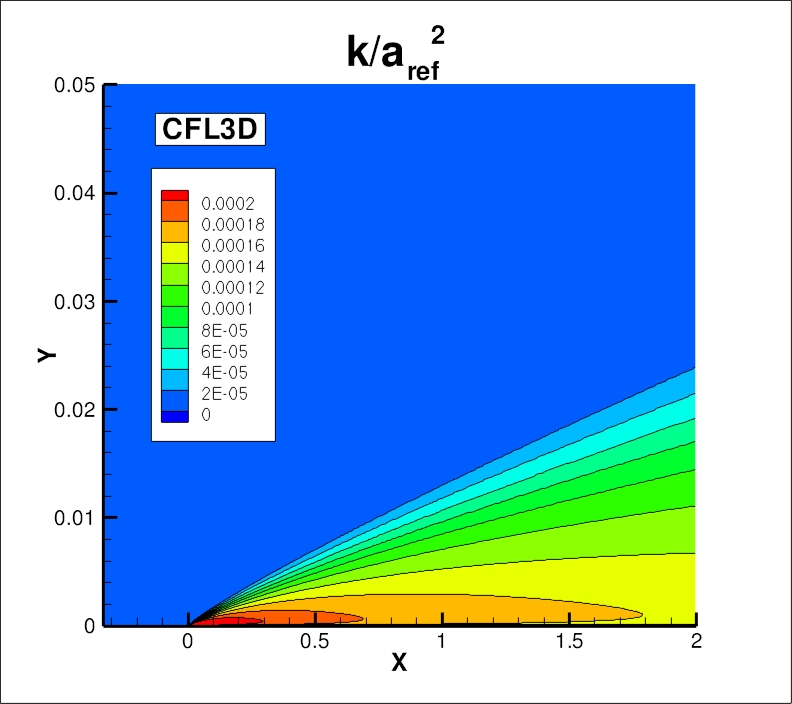
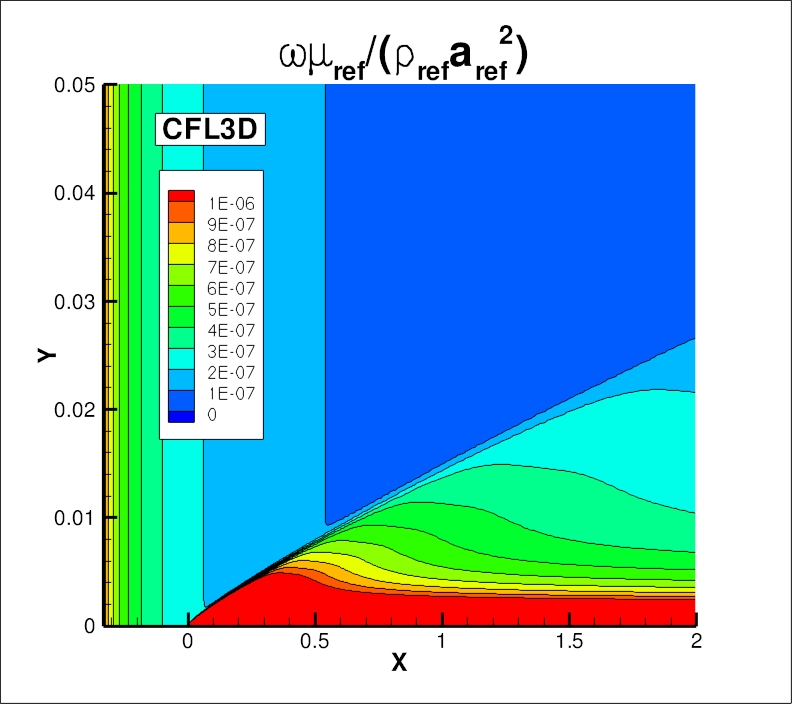
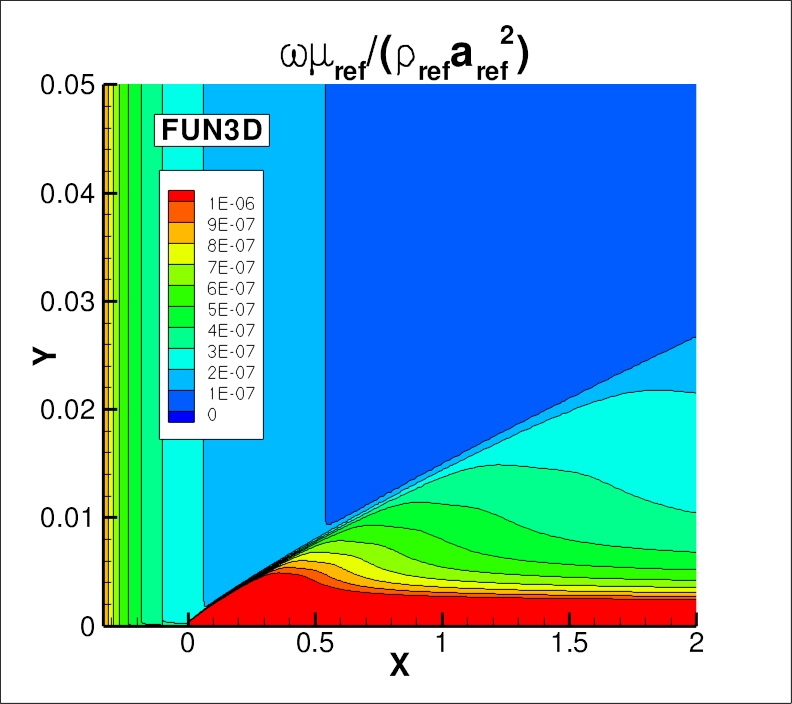
The nondimensionalized eddy viscosity contours, k contours, and omega contours
from the two codes on the finest 545 x 385 grid are shown
in the following plots (y-scale expanded for clarity).
Results from the two codes on this grid are essentially indistinguishable.
(Note legends do not necessarily reflect min and max values.)
The data files that generated the above plots are given here:
mut_contours_cfl3d_sstv.dat.gz (1.4 MB),
k_contours_cfl3d_sstv.dat.gz (1.4 MB),
omega_contours_cfl3d_sstv.dat.gz (1.4 MB) (structured,
at cell centers) and
mut_contours_fun3d_sstv.dat.gz (2.6 MB),
k_contours_fun3d_sstv.dat.gz (2.6 MB),
omega_contours_fun3d_sstv.dat.gz (2.6 MB) (unstructured,
at grid points). Note that these are all gzipped
Tecplot
formatted files, so you must either have Tecplot or know how to read their format in order to use these
files.
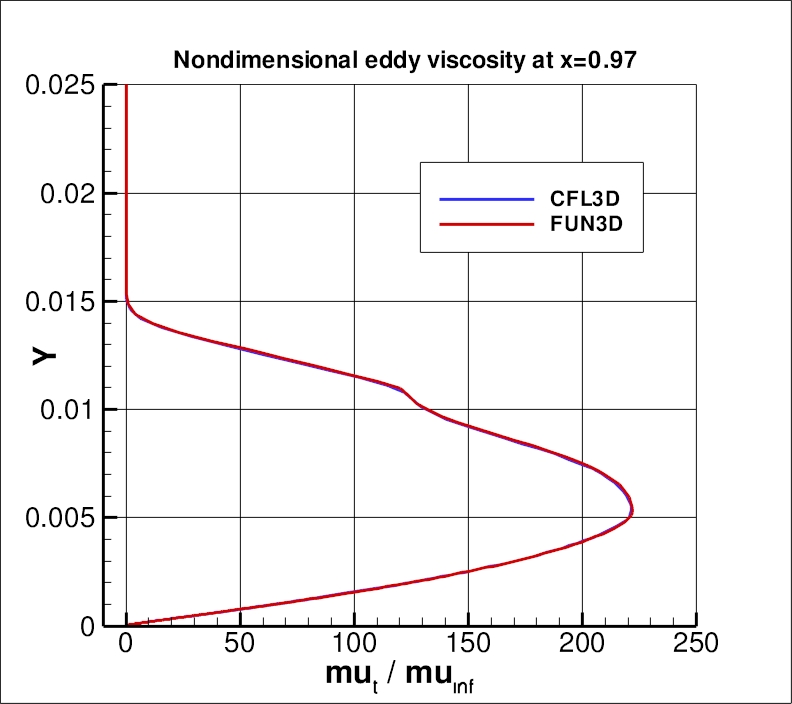
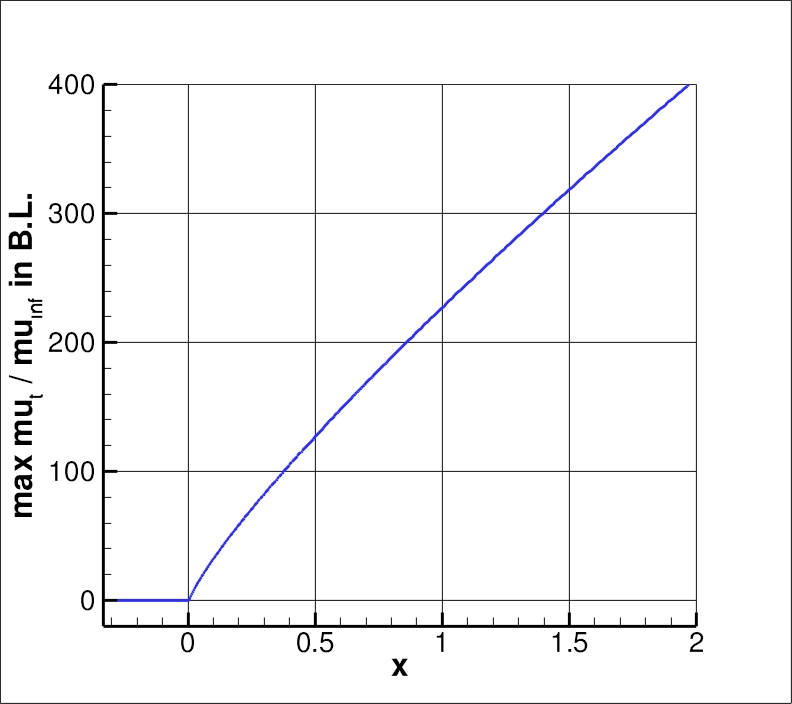
Using the finest 545 x 385 grid, an extracted nondimensional eddy viscosity profile at
x=0.97 is shown below, along with a plot of the maximum nondimensional
eddy viscosity as a function of x.
The data file that generated the eddy viscosity profile at x=0.97 is given here:
mut_0.97_sstv.dat.
The data file that generated the max eddy viscosity plot is given here:
find_peak_mut_sstv.dat (extracted only for CFL3D).
Notice that the nondimensional eddy viscosity above has a small "bump" near y=0.01 in the above plot.
The same behavior occurs for both CFL3D and FUN3D on the finest grid.
This behavior is due to the SST blending between omega and vorticity
in the denominator of the equation for eddy viscosity, and is only
noticeable on extremely fine grids for this flat plate case.
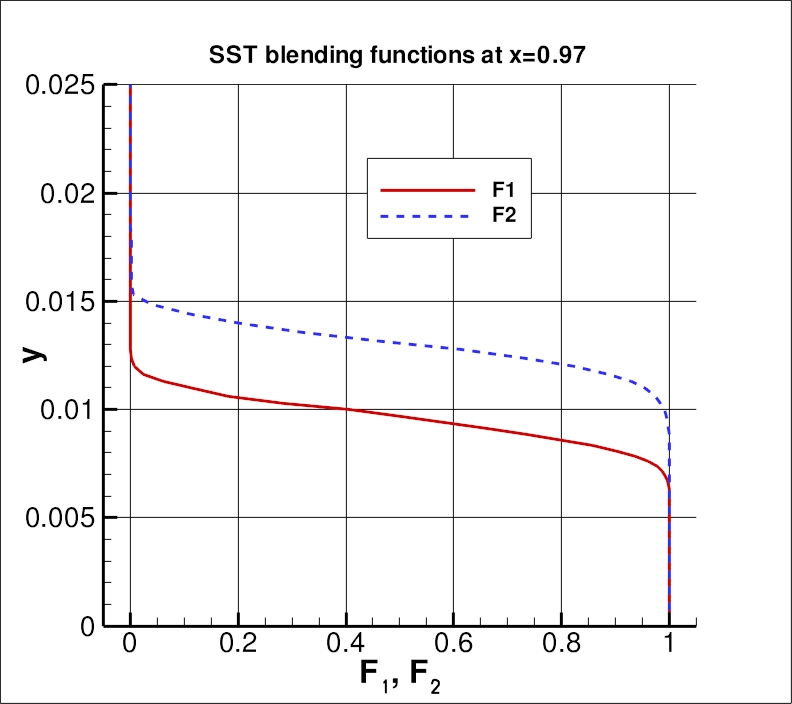
The bump is located in the region where the SST F1 and F2 functions are in the
process of transitioning from 1 to 0, as shown in
the following plot from the 545 x 385 grid.
The data file that generated the F1 and F2 profiles is given here:
sstv_f1f2_function.dat.
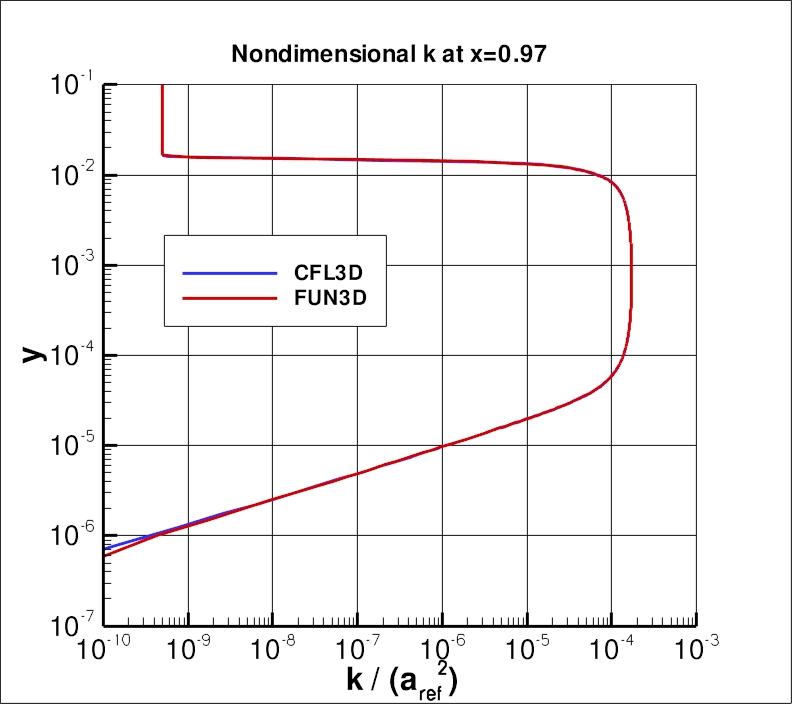
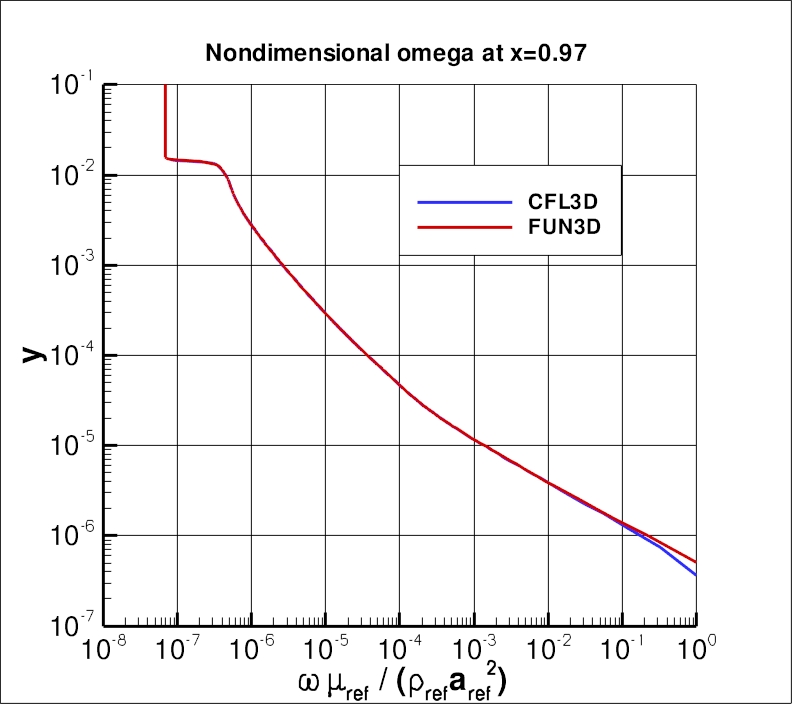
The nondimensional k and omega profiles at x=0.97008 from the 545 x 385 grid are shown in the following plots.
Note that the sharp behavior of these variables near the boundary layer edge
is one of the characteristics of this model (as well as others - see, e.g., Hellsten, A., "New Two-Equation
Turbulence Model for Aerodynamic Applications," PhD Thesis, Helsinki University of Technology,
Espoo, Finland, Feb 2004, pp. 96-103, available from
link to TKK dissertations). In cases where the grid resolution is not
as fine as it is here, numerical damping generally acts to smooth the sharp
behavior.
The data file that generated the nondimensional k and omega profiles at x=0.97 is given here:
sstv_omega_k.dat.
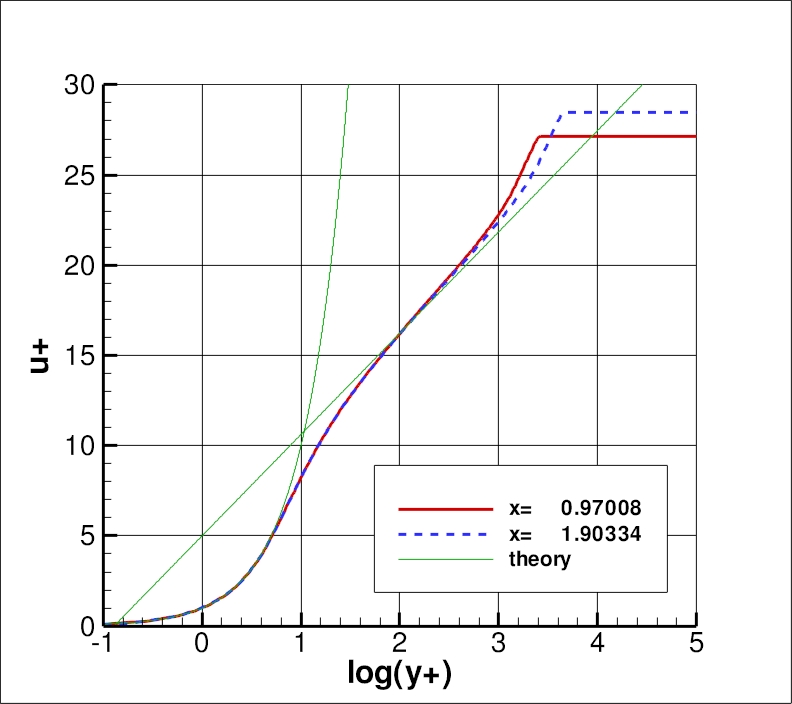
In terms of inner wall variables, u+ and y+, the finest grid yields the following results, which
are shown at two x-locations of x=0.97008 and x=1.90334. The
law-of-the-wall theory with kappa=0.41 and B=5.0 is also shown
(see White, F. M., Viscous Fluid Flow, McGraw-Hill Book Company, New York,
1974, p. 472).
The data file that generated the above plot is given in
flatplate_u+y+_sstv.dat for the CFD (extracted only for CFL3D), and in
u+y+theory.dat for the theory (other theoretical curves,
not shown in the plot, are also included in this latter file).
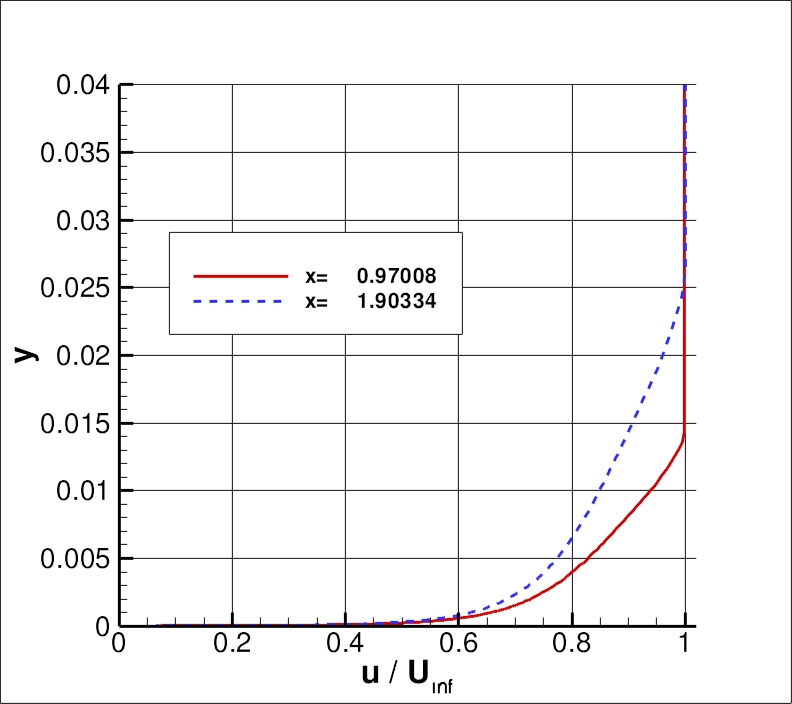
Standard velocity profiles are shown at the same two x-locations of x=0.97008 and x=1.90334 for
the finest grid in the following plot.
The data file that generated the above plot is given in
flatplate_u_sstv.dat (extracted only for CFL3D).
FUN3D was also run for this case using the same grids cut into triangles.
The following plot shows the convergence of the wall skin friction coefficient
at x=0.97008, compared to the earlier results on quad grids. The solution is
approaching the same result as the grid is refined.
The uncertainty estimation procedure applied to the "FUN3D, triangles" results yields:
| Code |
Computed apparent order, p |
Approx rel fine-grid error, ea21 |
Extrap rel fine-grid error, eext21 |
Fine-grid convergence index, GCIfine21 |
| FUN3D, triangles |
1.24 |
0.329% |
0.240% |
0.300% |
The data file that generated the "FUN3D, triangles" results in the above plot
is given in
cf_convergence_fun3d_sstv_tri.dat.
Results for total integrated drag coefficient using the triangular grids
are shown in the following plot, alongside the quad grid results.
The uncertainty estimation procedure applied to the "FUN3D, triangles" results yields:
| Code |
Computed apparent order, p |
Approx rel fine-grid error, ea21 |
Extrap rel fine-grid error, eext21 |
Fine-grid convergence index, GCIfine21 |
| FUN3D, triangles |
0.99 |
0.520% |
0.523% |
0.657% |
The data file that generated the "FUN3D, triangles" results in the above plot
is given in
drag_convergence_fun3d_sstv_tri.dat.
The surface skin friction coefficient on the finest 545 x 385 grid cut into
triangles is shown in the next plot. To plotting accuracy,
triangle-grid results are almost the same as the results
on the finest quad grid.
The data file that generated the "FUN3D, triangles" results in the
above plot is given here:
cf_plate_fun3d_sstv_tri.dat.
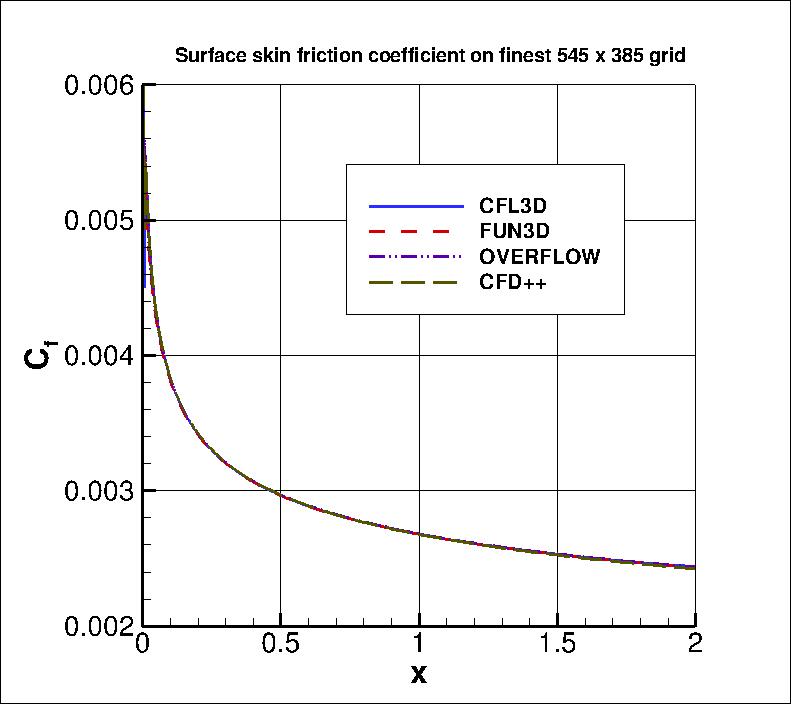
Other SST/SST-V/SST-Vm results using the independent codes
OVERFLOW, TURCOM, and CFD++ are shown below
(recall that SST, SST-V, and SST-Vm results are nearly identical in a given code
for this flat plate case).
NAS Technical Paper 2014-03 (pdf file)
(16.2 MB) by Childs, Pulliam, and Jespersen provides details of the OVERFLOW results for this case.
Recall that all results above (and elsewhere on this website) are from compressible CFD codes.
To give an indication of the magnitude of the difference between compressible (M=0.2) and incompressible results
using SST/SST-V/SST-Vm
for this case, sample skin friction convergence at x=0.97 using different compressible/incompressible codes are plotted below:
The data file of incompressible results from the above plot is given here:
cf_incomp_results_sstv.dat.
Below, the influence of a variety of different freestream turbulence conditions on the M=0.2 case
using SST/SST-V/SST-Vm is described.
Recall that the turbulent inflow boundary conditions used in CFL3D and FUN3D for all the results given above are:
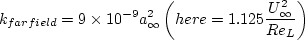
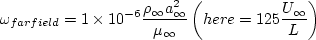
where the second equality in each equation is valid for the current problem only (M=0.2, Re=5 million).
For this case these correspond to freestream turbulence intensity=0.039% and freestream turbulent viscosity (relative to laminar)=0.009.
Other freestream levels were tested on the 273 x 193 grid in CFL3D, as tabulated here:
| Tu,% |
mu_t/mu_ref |
Cd |
Cf at x=0.97 |
% difference Cd from default |
% difference Cf from default |
| 0.01 |
0.009 (default) |
0.284569 |
0.00268311 |
0.004 |
0.004 |
| 0.039 (default) |
0.009 (default) |
0.284557 |
0.00268299 |
- |
- |
| 0.10 |
0.009 (default) |
0.284553 |
0.00268296 |
0.001 |
0.001 |
| 1.0 |
0.009 (default) |
0.284551 |
0.00268293 |
0.002 |
0.002 |
| 0.039 (default) |
0.001 |
0.284553 |
0.00268295 |
0.001 |
0.001 |
| 0.039 (default) |
0.1 |
0.284569 |
0.00268311 |
0.004 |
0.004 |
| 0.039 (default) |
1.0 |
0.284575 |
0.00268317 |
0.006 |
0.007 |
| 0.039 (default) |
10.0 |
0.284576 |
0.00268318 |
0.007 |
0.007 |
| 1.0 |
10.0 |
0.284816 |
0.00268528 |
0.09 |
0.09 |
The bottom line is that, within a "reasonable range," the
freestream turbulence levels made very little difference in the solution for this case (less
than 0.1% for all cases tested). For
fully turbulent solutions, the levels must be
sufficient to allow the model to activate turbulence early on the plate, but must not be
so unphysical as to corrupt the turbulent solutions (see discussion in
note 5 on Notes on running CFD page).
Note for users of OpenFOAM.
Return to: 2D Zero Pressure Gradient Flat Plate Verification Case Intro Page
Return to: Turbulence Modeling Resource Home Page
Recent significant updates:
08/28/2020 - changed SST-V naming to SST-Vm
12/05/2014 - added link to NAS Technical paper of OVERFLOW results for the verification cases
9/18/2014 - added link to note for users of OpenFOAM
1/21/2014 - renamed data files for consistency
7/15/2013 - added table showing effect of freestream turbulence
7/11/2013 - added comparison with incompressible results
Privacy Act Statement
Accessibility Statement
Responsible NASA Official:
Ethan Vogel
Page Curator:
Clark Pederson
Last Updated: 11/05/2021


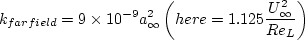
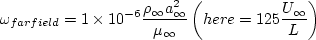
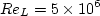 .
.
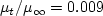 .
Although these levels are different from the range quoted in the
original SST reference,
tests were also done with the following levels that fall within the original SST author's recommended range:
.
Although these levels are different from the range quoted in the
original SST reference,
tests were also done with the following levels that fall within the original SST author's recommended range:
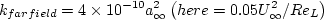 , and
, and
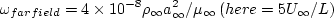 . The resulting freestream turbulent eddy viscosity ends up
about the same:
. The resulting freestream turbulent eddy viscosity ends up
about the same:
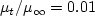 .
Computed results were almost identical (for example, both
Cf in the middle of the plate and total CD differed by well less than
one percent). See further discussion near the bottom of the page (below) on influence of freestream
turbulence levels for this case.
.
Computed results were almost identical (for example, both
Cf in the middle of the plate and total CD differed by well less than
one percent). See further discussion near the bottom of the page (below) on influence of freestream
turbulence levels for this case.