skip to content

NASA Logo

Langley Research Center

Turbulence Modeling Resource

 

Return to: Turbulence Modeling Resource Home Page


 

VERIF/3DB: 3D Bump-in-channel Verification Case - Intro Page

The purpose here is to provide a large sequence of nested grids of the same family, along with results from existing CFD codes that employ specific forms of particular turbulence models, in order to help programmers verify their implementations of these same models. On a given grid, there may be differences between the results from different codes, but presumably as the grid is refined the results should approach the same answer (if the flow conditions and boundary conditions are the same). With verification, the purpose is not to establish the "goodness" of a model compared to experiment, but rather to establish that a model has been implemented correctly, as intended according to the equations and boundary conditions. (It is through validation that a model's "goodness" is established.) The purpose here is primarily verification.

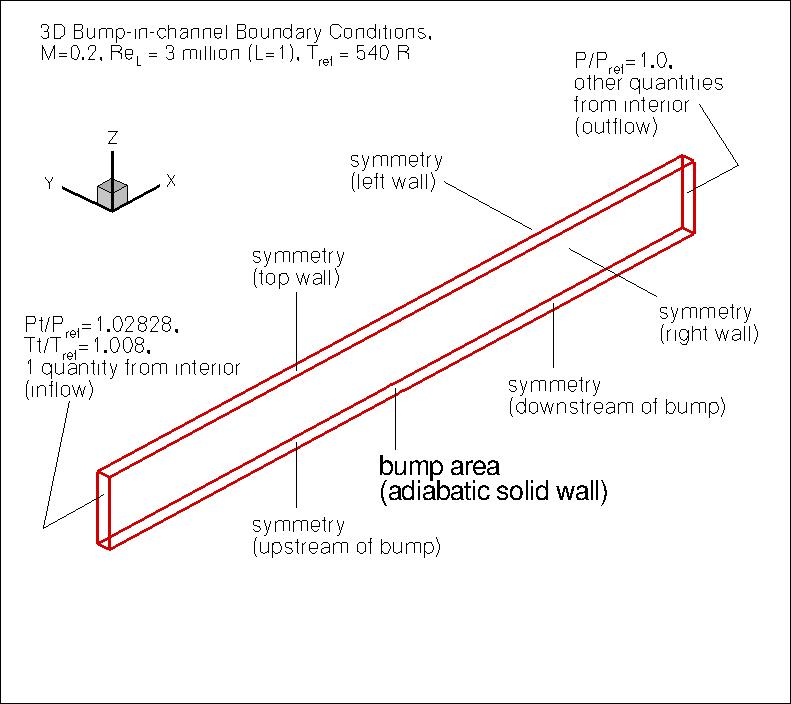
The 3D bump-in-channel case is a three-dimensional version of the 2D bump-in-channel verification case, with spanwise variation added. In this 3D case the z direction is "up" and y is "spanwise." It was run at M = 0.2, at a Reynolds number of Re = 3 million based on length "1" of the grid. The body reference area is 1.5 units. This lower wall is a curved viscous-wall bump extending from x=0 to 1.5 at the two sides of the computational domain y=0 and y=-1, but starting and ending further downstream at y locations inbetween. 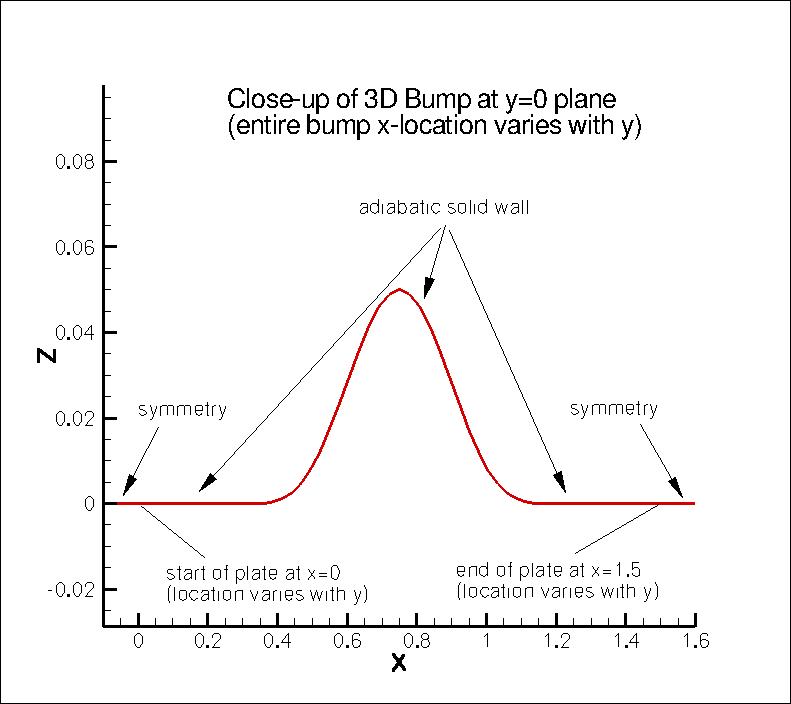The maximum bump height is 0.05. The "2D" definition of the bump at the y=0 plane is:

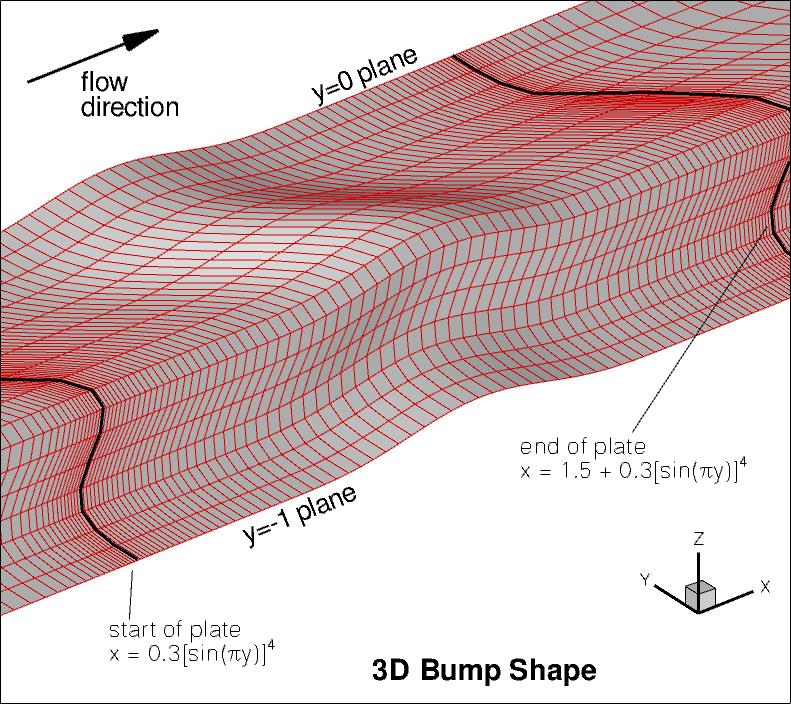
But the x-location of any position on the bump varies in the spanwise direction between y=0 and y=-1 according to:

where x0 is any given x-location of the "2D" shape at y=0, and "pi"=3.1415927... The upstream and downstream farfield extends 25 units from the viscous-wall, with symmetry plane BCs imposed on the lower wall between the farfield and the solid wall. The upper boundary is a distance of z=5.0 high. It is taken to be a symmetry plane. The left and right walls are also taken to be symmetry planes. The following plots show the layout of this case, along with the boundary conditions. (Note that particular variations of the BCs at the inflow, top wall, outflow, and side walls may also work and yield similar results for this problem.)

Another important note: although M=0.2 is low enough that the flow is "essentially" incompressible, this is a compressible flow verification case. Therefore, if you run this case with an incompressible code, your results may be close - but not quite the same - as the grid is refined.

bump grid layout & BCs close-up of bump picture of bump shape


 

What to Expect:
RESULTS
 LINK TO EQUATIONS
 MRR Level
SA
 SA eqns
 4
SA-RC-QCR2000
 SA-RC-QCR2000 eqns
 3
SST-Vm
 SST-Vm eqns
 3
SSG/LRR-RSM-w2012
 SSG/LRR-RSM-w2012 eqns
 3
Wilcox2006-klim-m
 Wilcox2006-klim-m eqns
 2

(Other turbulence model results may be added in the future.)
 
 

Return to: Turbulence Modeling Resource Home Page


 
 

Recent significant updates:
08/28/2020 - changed SST-V naming to SST-Vm
02/25/2014 - added Wilcox2006 page

Privacy Act Statement

Accessibility Statement

Responsible NASA Official: Ethan Vogel
Page Curator: Clark Pederson
Last Updated: 03/23/2021