For this flow, an odd-even decoupling occurs in FUN3D on the finest grid using the default unweighted least-square
gradient. This decoupling is particularly noticeable, for example, in plots of Cp along a spanwise grid line
somewhat upstream of the bump peak.
Preliminary studies indicate the decoupling is associated with gradients near the inflection point
in the bump surface.
Although not done for the results below, the decoupling can be eliminated in FUN3D
by using a mapping method based on distance from the surface for
the mean flow inviscid fluxes. See the
3D Modified Bump-in-channel Validation case
for SA-neg in the Turbulence Model Numerical Analysis section of this website.
Also see AIAA paper 2016-0858,
https://doi.org/10.2514/6.2016-0858.
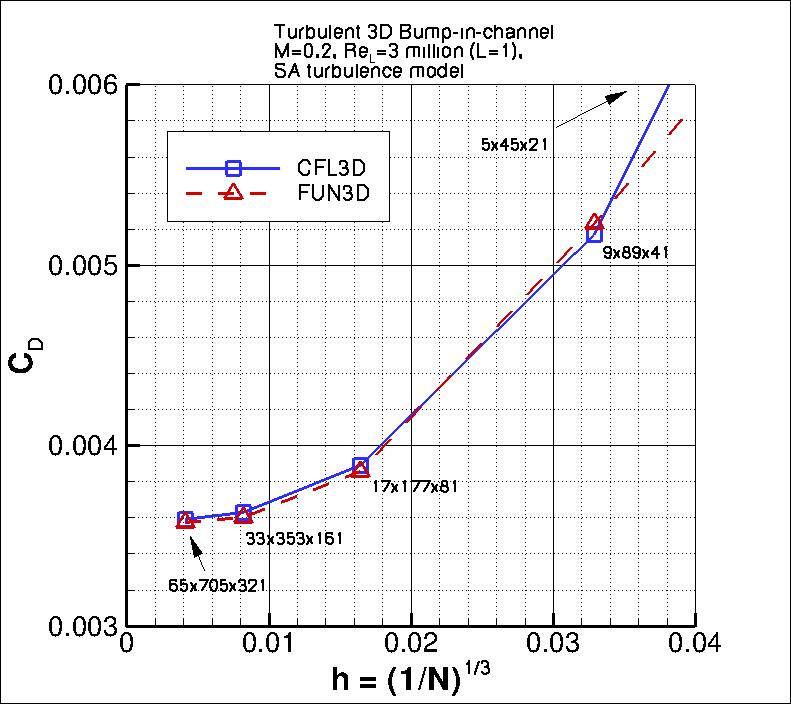
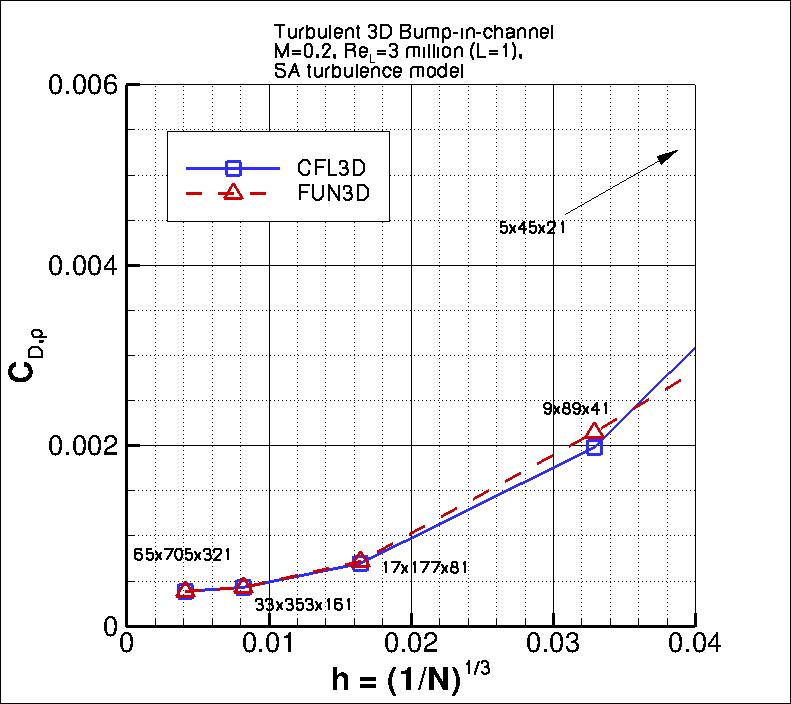
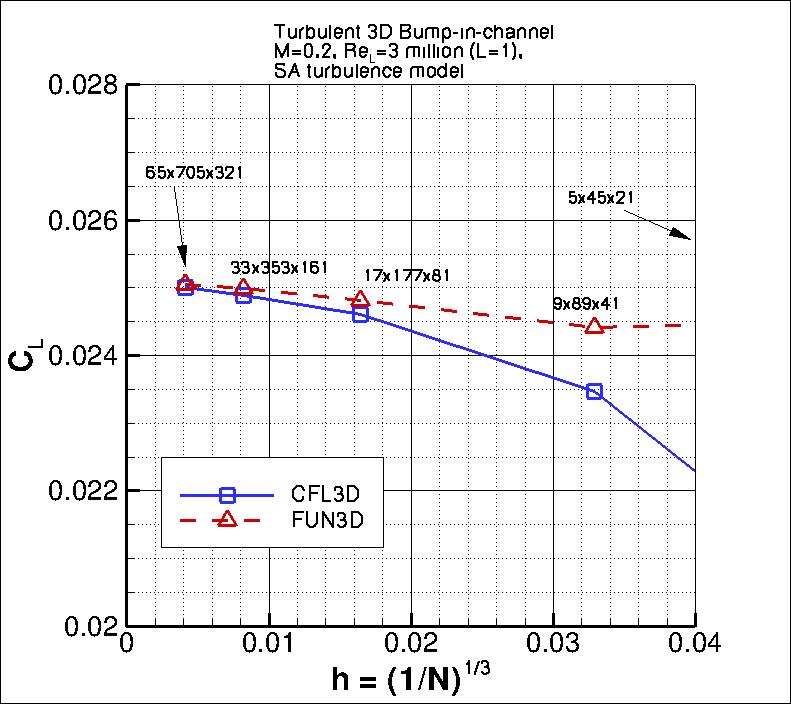
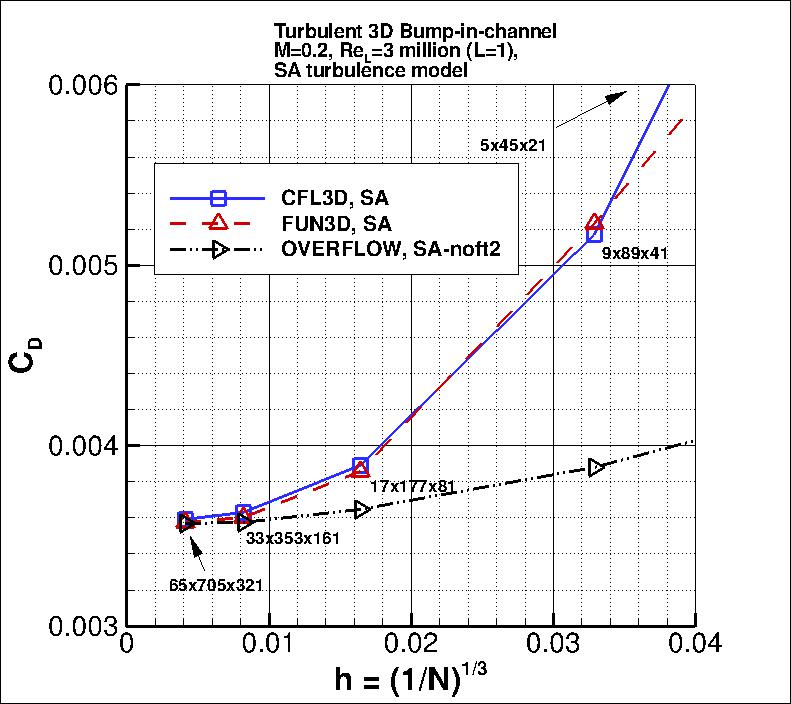
The following plots show: (1) total drag coefficient, (2) pressure drag coefficient,
(3) viscous drag coefficient, and (4) total lift coefficient for the 3D bump.
Both codes are tending toward similar integrated force coefficient values
as the grid is refined.
Using the uncertainty estimation procedure from the Fluids Engineering Division of the ASME (Celik, I. B.,
Ghia, U., Roache, P. J., Freitas, C. J., Coleman, H., Raad, P. E.,
"Procedure for Estimation and Reporting of Uncertainty Due
to Discretization in CFD Applications," Journal of Fluids Engineering, Vol. 130, July 2008, 078001, https://doi.org/10.1115/1.2960953), described in Summary of Uncertainty Procedure,
the finest 3 grids yield the following:
| Code |
Quantity |
Computed apparent order, p |
Approx rel fine-grid error, ea21 |
Extrap rel fine-grid error, eext21 |
Fine-grid convergence index, GCIfine21 |
| CFL3D |
Cd |
2.76 |
1.083% |
0.188% |
0.234% |
| CFL3D |
Cd,p |
2.75 |
10.519% |
1.872% |
2.297% |
| CFL3D |
Cd,v |
2.45 |
0.048% |
0.011% |
0.013% |
| CFL3D |
CL |
1.34 |
0.448% |
0.293% |
0.367% |
| FUN3D |
Cd |
3.25 |
0.759% |
0.089% |
0.111% |
| FUN3D |
Cd,p |
2.74 |
11.299% |
2.033% |
2.491% |
| FUN3D |
Cd,v |
0.93 |
0.510% |
0.561% |
0.705% |
| FUN3D |
CL |
1.45 |
0.245% |
0.141% |
0.177% |
The data file that generated the above plots is given here:
force_convergence_sa.dat.
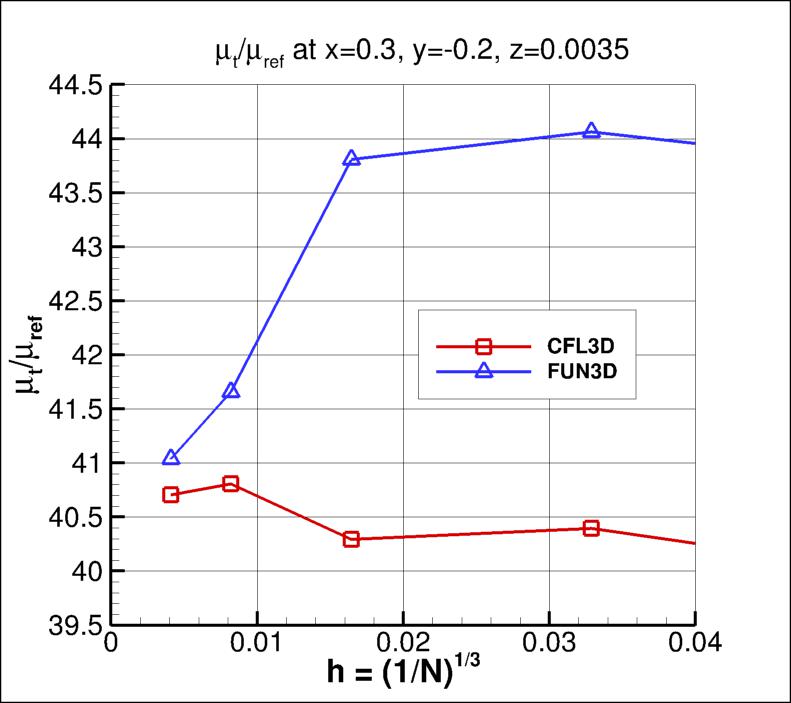
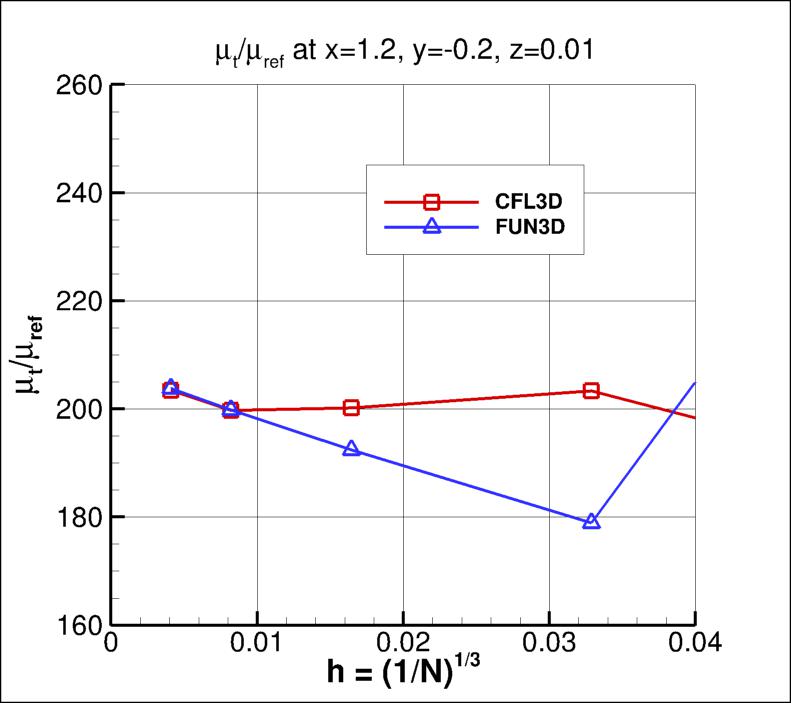
The nondimensional eddy viscosity at two particular locations in the flowfield are examined next, as
a function of grid. Again, as the grid is refined (i.e., as h approaches 0), results from both codes appear to be
approaching approximately the same result.
Using the same uncertainty estimation procedure as above,
the finest 3 grids yield the following:
| Code |
Quantity |
Computed apparent order, p |
Approx rel fine-grid error, ea21 |
Extrap rel fine-grid error, eext21 |
Fine-grid convergence index, GCIfine21 |
| CFL3D |
mu_t/mu_ref at x=0.3 position |
oscillatory convergence |
0.254% |
N/A |
N/A |
| CFL3D |
mu_t/mu_ref at x=1.2 position |
oscillatory convergence |
1.794% |
N/A |
N/A |
| FUN3D |
mu_t/mu_ref at x=0.3 position |
1.79 |
1.517% |
0.621% |
0.772% |
| FUN3D |
mu_t/mu_ref at x=1.2 position |
0.87 |
1.978% |
2.340% |
2.996% |
The data file that generated the above plots is given here:
eddy_convergence_sa.dat.
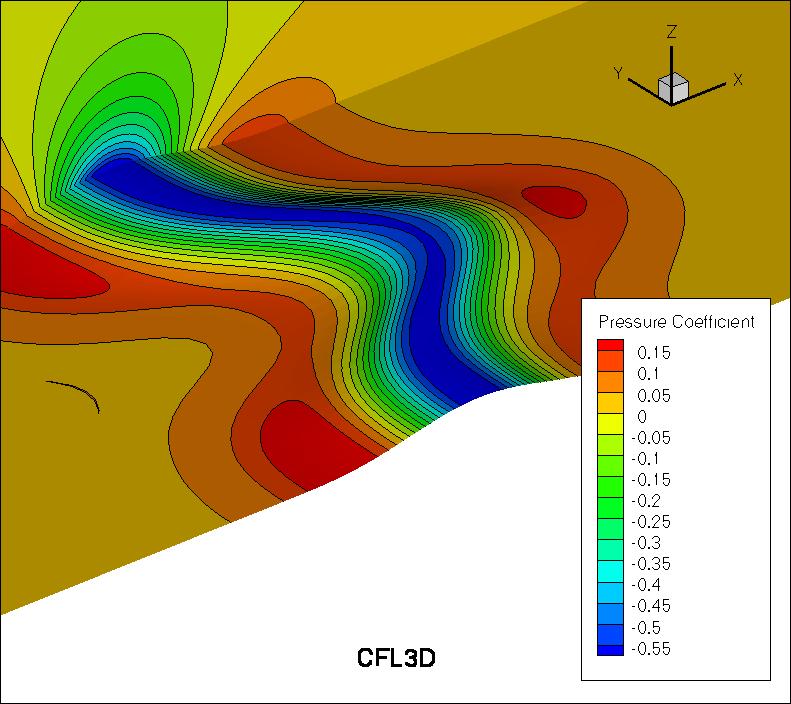
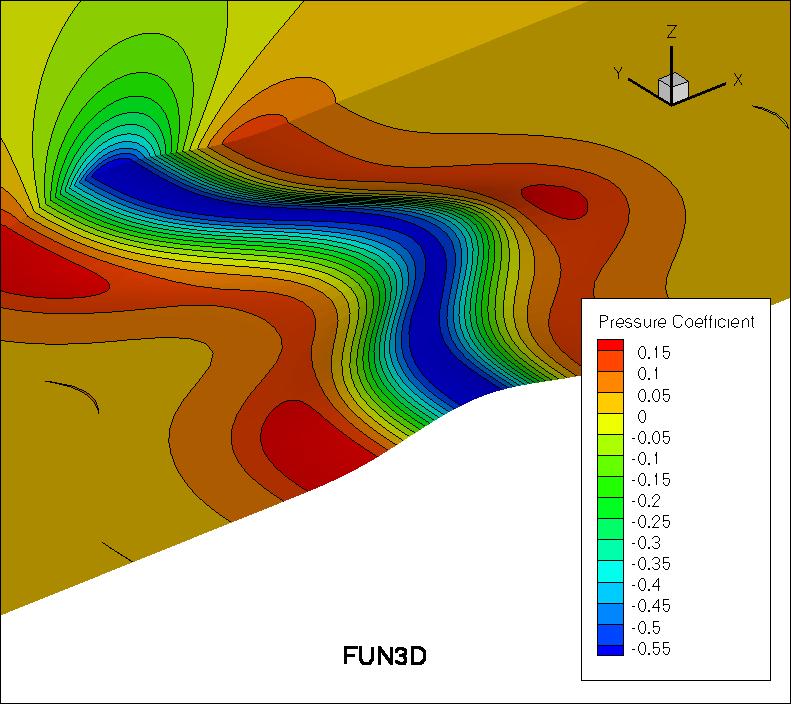
The surface pressure coefficient from both codes on the second-finest
33 x 353 x 161 grid
over the bump wall and at y=0 is shown in the next plots.
Both codes yield nearly identical results.
The data files that generated the above plots are given here:
cp_surface_sa_cfl3d.dat.gz,
cp_y0_sa_cfl3d.dat.gz,
cp_surface_sa_fun3d.dat.gz,
cp_y0_sa_fun3d.dat.gz.
Note that these are all gzipped
Tecplot
formatted files, so you must either have Tecplot or know how to read their format in order to use these
files.
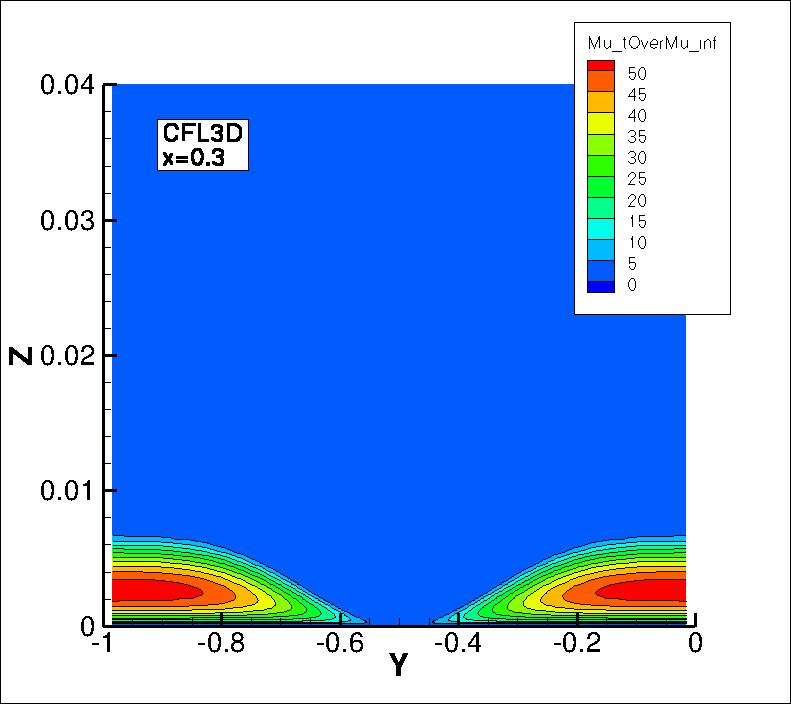
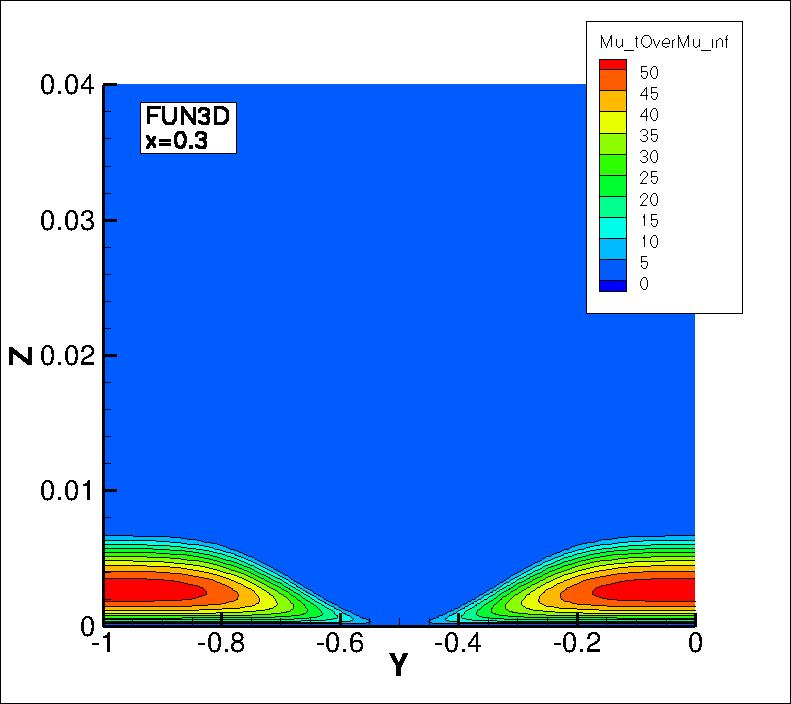
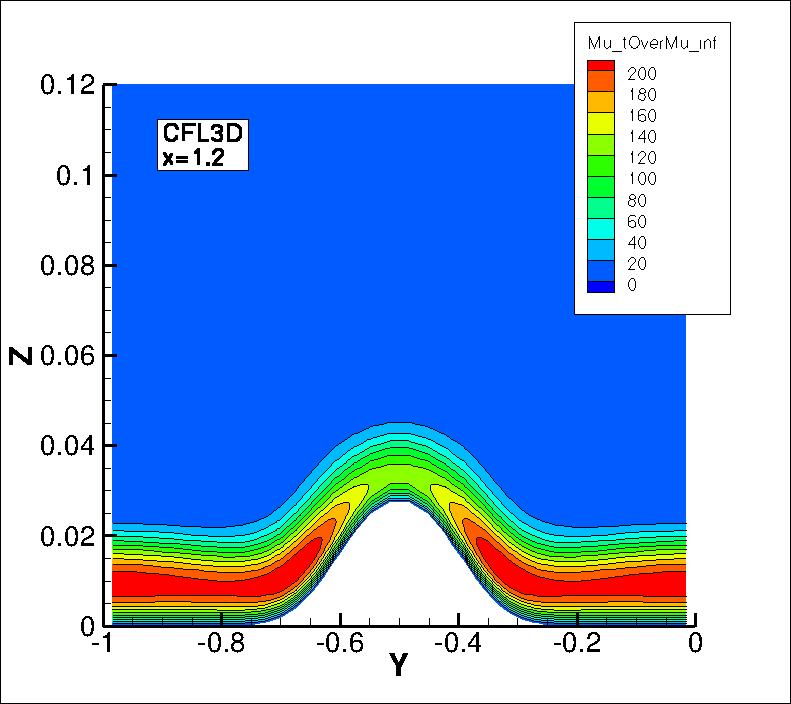
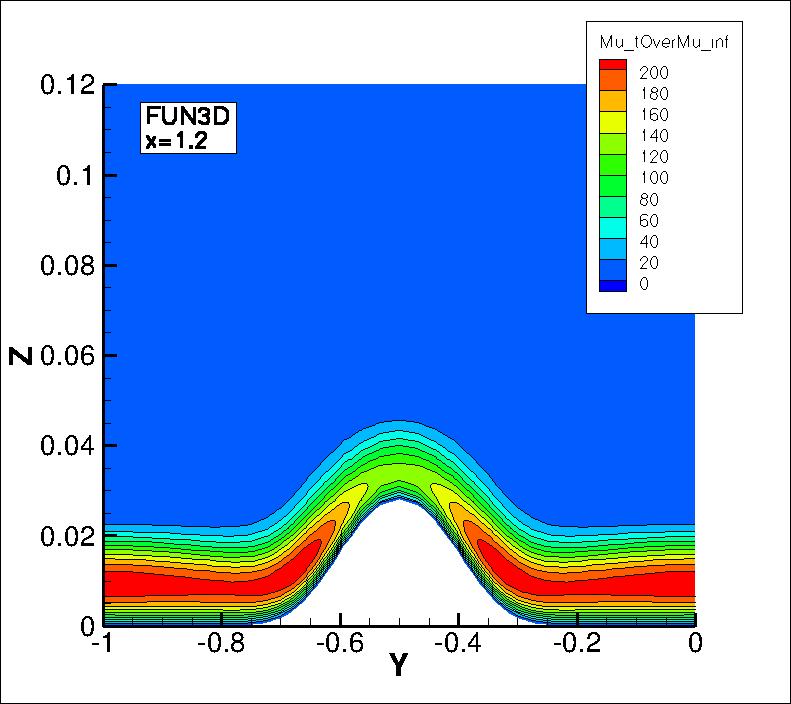
The eddy viscosity contours (nondimensionalized by freestream laminar viscosity)
from the two codes on the second-finest 33 x 353 x 161 grid are shown
in the following plots, extracted at two different x-locations
(z-scale expanded for clarity). Results from the two codes are essentially indistinguishable.
(Note legends do not necessarily reflect min and max values.)
The data files that generated the above plots are given here:
mut_0.3_cfl3d.dat.gz,
mut_0.3_fun3d.dat.gz,
mut_1.2_cfl3d.dat.gz,
mut_1.2_fun3d.dat.gz.
Note that these are all gzipped
Tecplot
formatted files, so you must either have Tecplot or know how to read their format
in order to use these files.
Also note that the slicing tool in Tecplot was used to generate this data,
extracting data along x-constant planes. These cutting planes do not necessarily
coincide with grid locations. Thus, the x, y, and z locations
given in the data files do not reflect actual points in
the grid used.
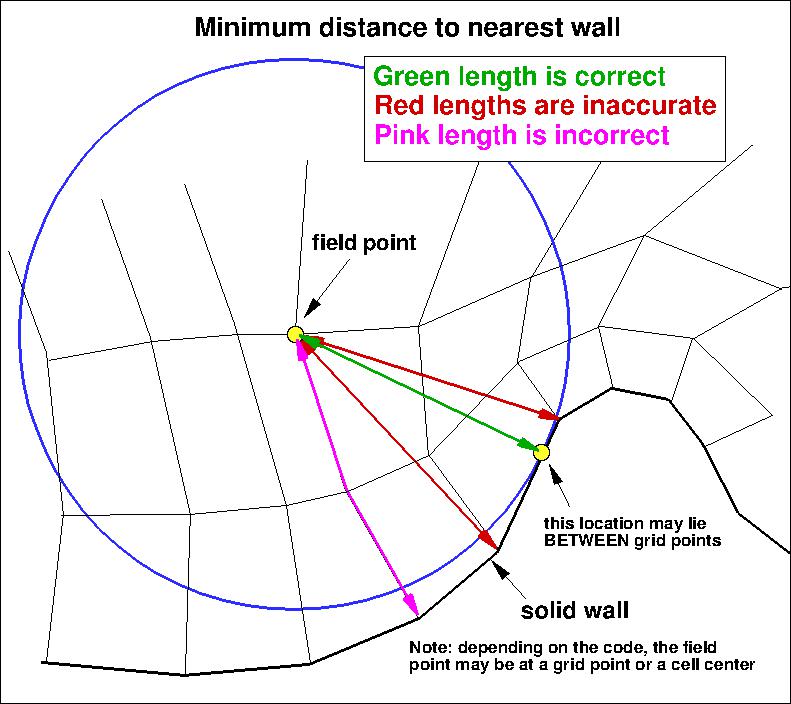
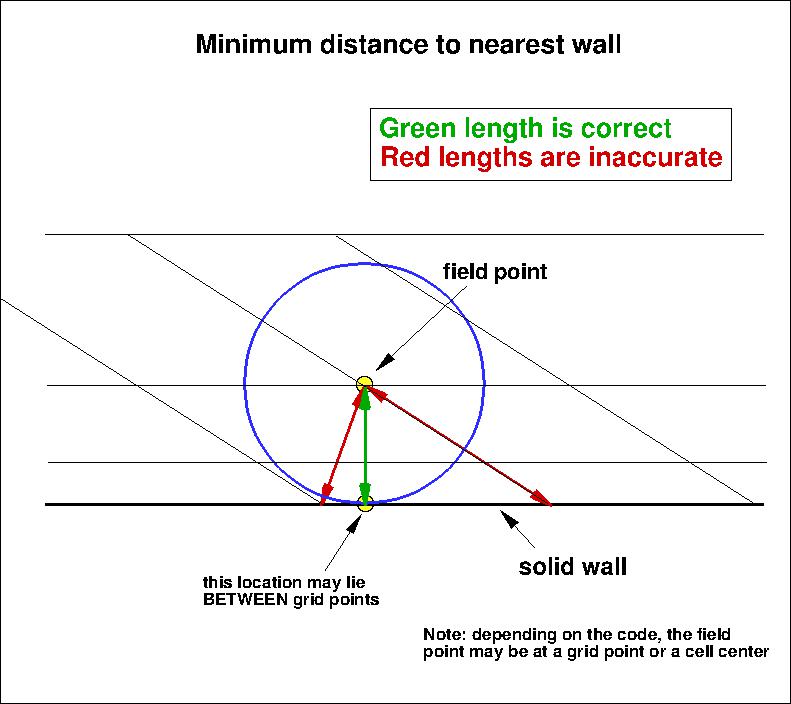
The SA model relies on the minimum distance to the nearest wall.
It is important to note that computing minimum distance by searching along grid lines is
incorrect, and is not the same as computing actual minimum distance to the nearest wall for this grid.
The following sketches
demonstrate the concept of minimum distance (in 2-D). Improperly-calculated minimum distance
functions will particularly produce incorrect results for cases in which the
grid lines are not perfectly normal to the body surface.
Note that when the nearest wall point is a sharp convex corner or edge (like an airfoil or wing trailing edge) then the
correct minimum distance is the distance to that corner or edge, which is not a wall normal.
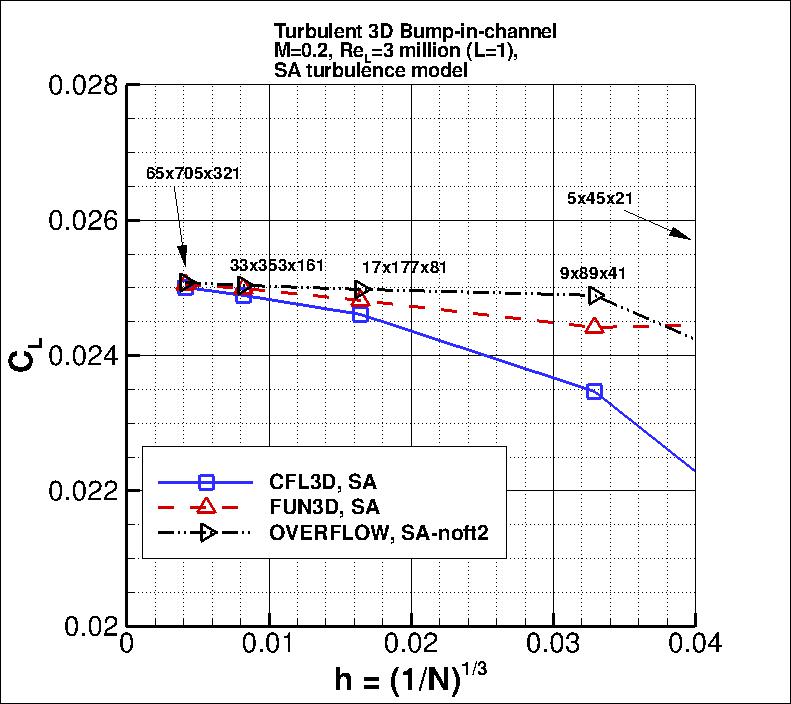
Results from OVERFLOW are shown alongside the CFL3D and FUN3D results below
(note that SA-noft2 yields essentially identical results for this case as SA).
NAS Technical Paper 2014-03 (pdf file)
(16.2 MB) by Childs, Pulliam, and Jespersen provides details of the OVERFLOW results for this case.
Note for users of OpenFOAM.
Return to: 3D Bump-in-channel Verification Case Intro Page
Return to: Turbulence Modeling Resource Home Page
Recent significant updates:
02/18/2021 - added plots (and data) of eddy viscosity convergence at two paticular locations in the flowfield
07/18/2018 - added note regarding odd-even decoupling in FUN3D on finest grid for this case
12/05/2014 - added link to NAS Technical paper of OVERFLOW results for the verification cases
Privacy Act Statement
Accessibility Statement
Responsible NASA Official:
Ethan Vogel
Page Curator:
Clark Pederson
Last Updated: 03/01/2023

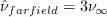 .
In both CFL3D and FUN3D, this was not the default setting, so special keywords needed to be
set in both codes.
For the interested reader, typical input files for this problem are given here:
.
In both CFL3D and FUN3D, this was not the default setting, so special keywords needed to be
set in both codes.
For the interested reader, typical input files for this problem are given here: