 |
Langley Research CenterTurbulence Modeling Resource |
Return to: Turbulence Modeling Resource Home Page
2DZPH: 2D Zero Pressure Gradient High Mach Number Flat Plate Validation Case
The purpose here is to provide a validation
case for turbulence models. Unlike verification, which seeks to establish that a model has been implemented
correctly, validation compares CFD results against data in an effort to establish a model's
ability to reproduce physics. A large sequence of nested grids
of the same family are provided here if desired. Data are also provided for comparison.
For this particular flat plate case, the data are from theory.
For the grids given below, running at a Reynolds number per unit length of Re = 15 million
is sufficient to achieve desired Retheta levels, and to allow the turbulence
models to fully activate far enough upstream.
The following plot shows the layout of the simple
flat plate grids, along with typical boundary conditions for supersonic flow.
(Note that particular variations of the BCs at the inflow, top wall, and outflow
may also work and yield similar results for this problem.)
Note: at high Mach numbers (e.g., M > 2), CFD transition to fully turbulent wall-bounded flow can be delayed
compared with flow at lower M. Also, the delayed transition location can vary significantly with
the freestream levels set. See, for example, Journal of Spacecraft and Rockets, Vol. 47, No. 1, 2010, pp. 11-20,
https://doi.org/10.2514/1.45350 and
AIAA Journal, Vol. 47, No. 4, 2009, pp. 982-993,
https://doi.org/10.2514/1.39947 (which is based on
AIAA Paper 2008-4403).
For this test case, results are only plotted for regions of the flow that were fully turbulent.
GRIDS
(same as those used for
Flat Plate Verification case)
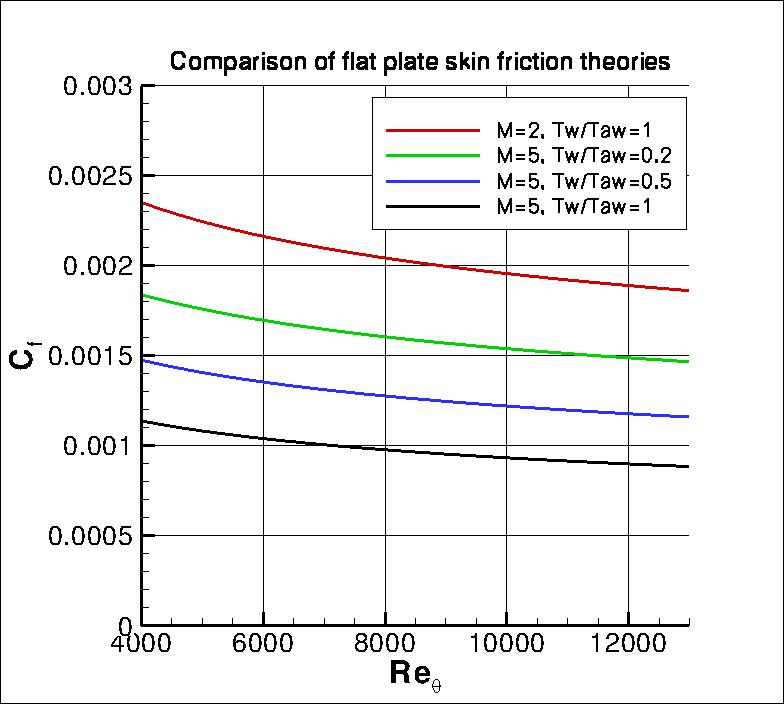
The following supersonic flat plate cases are under consideration:
Two quantities of interest are desired for comparison:
(It is worth noting that the second case - M=5, Tw/Taw approx 0.2 - tends
to exhibit greater grid sensitivity in its CFD results than the other cases for wall skin friction coefficient.)
Definitions are given here for the relevant quantities, including
Retheta, Cf, u+, and y+
It should be noted that computing Retheta typically involves an additional post-processing
step for many CFD codes (numerically integrating to obtain theta). Although this
step is relatively straightforward for the flat plate, nonetheless some numerical errors
are unavoidably introduced which may vary depending on the postprocessing program employed.
When viewing comparisons, this additonal potential source of error should be taken into
consideration. The so-called van Driest transformations (see, e.g., White, F. M., "Viscous Fluid Flow,"
McGraw-Hill, 1974, New York, pp. 632 ff) are used to obtain theoretical correlations for the
compressible wall skin friction coefficient and wall variables.
For incompressible wall skin friction, the Karman-Schoenherr (K-S) relation
(Schoenherr, K. E., Trans. SNAME. 40:279-313, 1932) is:
The van Driest II transformation can be used to transform the incompressible levels
to levels valid for supersonic flows with various wall temperatures.
Details are as follows:
The approximate adiabatic wall temperature is:
where r=0.89 is the recovery factor (an empirical factor introduced because in practice energy recovery
is not perfect). The compressible skin friction is related to the incompressible value in van Driest II via:
Using Sutherland's law, this becomes:
For
u+ vs. y+, the incompressible law-of-the-wall based on Coles' mean velocity profile
(Coles, D., J. Fluid Mech. 1(2):191-226, 1956,
https://doi.org/10.1017/S0022112056000135
Coles, D., RAND Corp Rept. R-403-PR, 1962,
https://www.rand.org/pubs/reports/R403.html),
is:
The van Driest I transformation can be used to transform the incompressible
law-of-the-wall to one valid for supersonic flows with various wall temperatures. Details are as follows.
The transformation uses:
Note that the theoretical correlations are imperfect. Not only is there some uncertainty in
the incompressible correlations themselves (see discussion on the
Subsonic Flat Plate Validation Case webpage), but there is further
uncertainty about the best transformations for producing compressible correlations (see, e.g.,
White, F. M., "Viscous Fluid Flow," McGraw-Hill, New York, 1974). For example,
the van Driest II transformation may yield too-high skin friction for strongly-cooled walls
(Huang, P. G., Bradshaw, P., and Coakley, T. J., AIAA Journal, Vol. 31, No. 9, Sept. 1993, pp. 1600-1604,
https://doi.org/10.2514/3.11820).
Results from the van Driest transformations are plotted in the following figures, using
freestream temperature of 300K and standard air conditions:
The data files for these correlations are provided here:
What to Expect:
(Other turbulence model results may be added in the future.)
Note that the OVERFLOW code has documented its results for this validation case (for the SA-noft2 and SST-V
turbulence models) in NAS Technical Paper 2016-01 (pdf file)
(18.3 MB) by Jespersen, Pulliam, and Childs.
Return to: Turbulence Modeling Resource Home Page
Recent significant updates: Responsible NASA Official:
Ethan Vogel

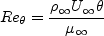
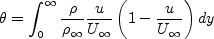
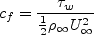

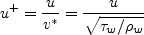
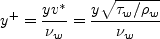
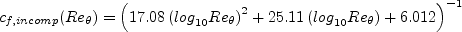

where:
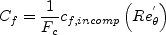
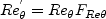
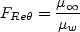
where temperatures are in degrees K. Other correlation parameters are:

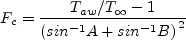
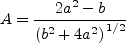
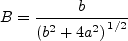
![a=\left(r\frac{\gamma-1}{2}M^{2}\frac{T_\infty}{T_w}\right)^{1/2}=\left[\left(\frac{T_{aw}}{T_\infty}-1\right)\frac{T_\infty}{T_w}\right]^{1/2}](ZPGflatplate_eqns/img17.png)
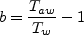
along with a van Driest type damping near the wall.
A program provided by P. G. Huang was used to compute these mean incompressible profiles.
See Bardina et al, NASA TM 110446, April 1997,
https://ntrs.nasa.gov/citations/19970017828
for more details.
![u^+_{incomp} = \frac{1}{\kappa} {\rm ln} \left( y^+ \right) + C + \frac{2 \Pi}{\kappa}
\left[ {\rm sin} \left( \frac{\pi y}{2 \delta} \right) \right]^2](ZPGflatplate_eqns/img9.png)
so that:
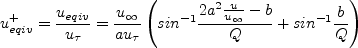
where:
![u^{+}=\frac{u}{u_\tau}=\frac{u_\infty}{2u_{\tau}a^2}\left[Q*sin\left(\frac{au_\tau}{u_\infty}u_{incomp}^{+}-sin^{-1}\frac{b}{Q}\right)+b\right]](ZPGflatplate_eqns/img22.png)

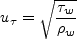
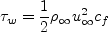
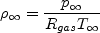
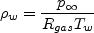
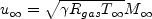

RESULTS
LINK TO EQUATIONS
MRR Level
SA
SA eqns
4
SST-Vm
SST-Vm eqns
3
Wilcox2006-klim-m
Wilcox2006-klim-m eqns
2
EASMko2003-S
EASMko2003-S eqns
1
K-e-Rt
K-e-Rt eqns
1
03/21/2023 - mentioned possible delay in transition to fully turbulent flow at higher M
08/28/2020 - changed SST-V naming to SST-Vm
Page Curator:
Clark Pederson
Last Updated: 03/12/2025